Another Rightmost Long Division
Logic
Level
2
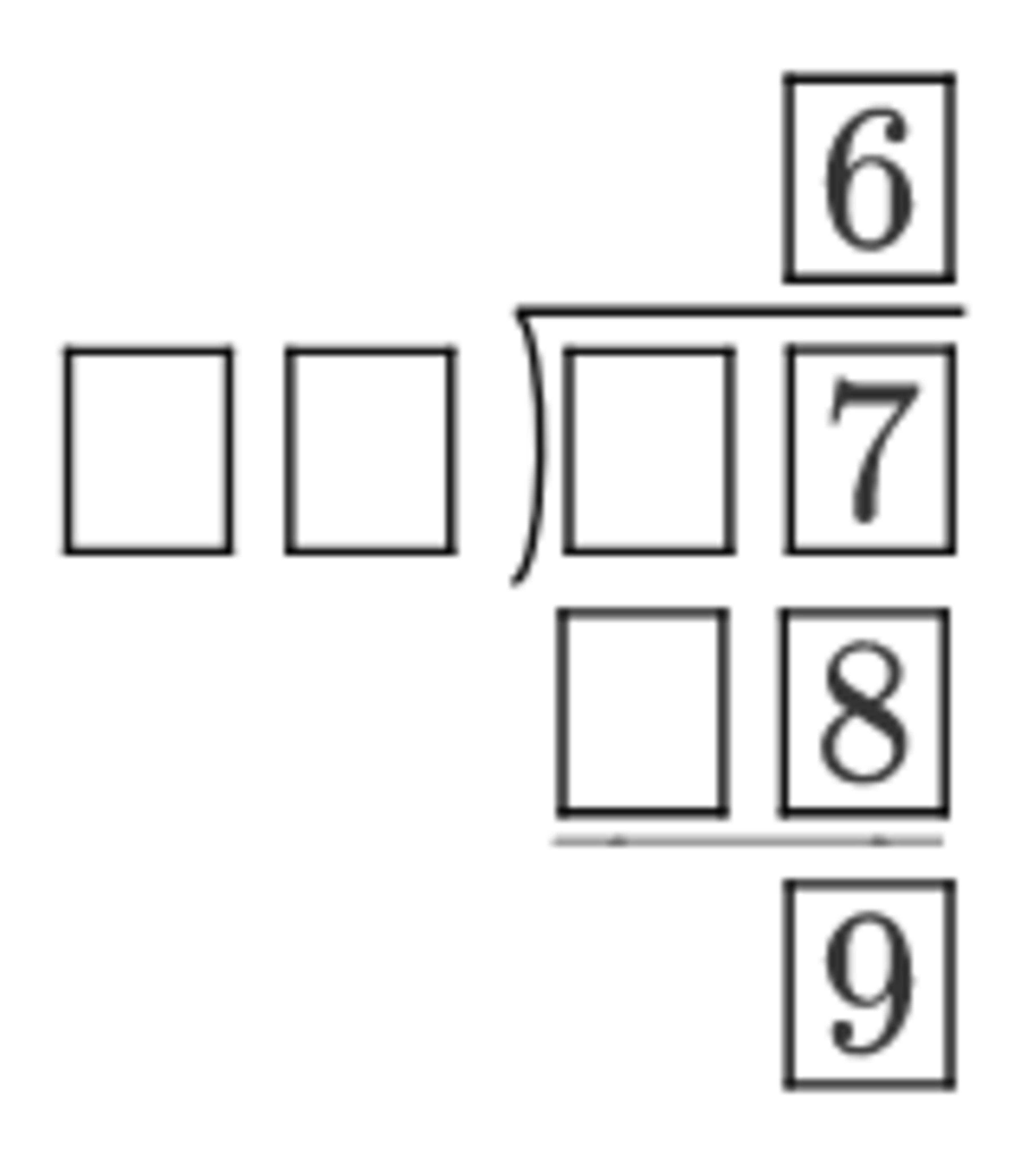
Above shows a long division. What is the sum of all the missing digits?
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 6 0 0 \enclose l o n g d i v 0 7 0 8 9
Looking at the red highlighted numbers as shown above, we see that a 2-digit positive integer multiply by 6 gives another 2-digit integer. Let x and y denote these aforementioned integers respectively, then 6 x = y < 1 0 0 . So 6 x < 1 0 0 or equivalently x < 6 1 0 0 = 1 6 + 3 2 . Thus x = 1 0 , 1 1 , 1 2 , … , 1 6 only.
Since the multiplication of x and 6 gives a last digit of 8, then by trial and error, of all the numbers 1 0 , 1 1 , … , 1 6 , only 1 3 satisfy this constraint. hence x = 1 6 and so y = 6 x = 7 8 . We can now fill in some some brackets in the long division:
0 6 1 3 \enclose l o n g d i v 0 7 7 8 9
Looking at the blue highlighted numbers. We know that 0 7 − 7 8 = 9 , or equivalently 0 7 = 7 8 + 9 = 8 7 , thus the remaining missing digit is 8. And now we can complete the entire long division:
0 6 1 3 \enclose l o n g d i v 8 7 7 8 9
The sum of all the missing digits is 1 + 3 + 8 + 7 = 1 9 .