another russian log problem
Algebra
Level
4
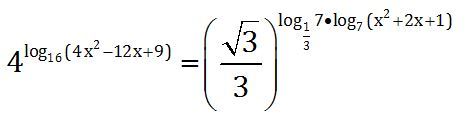 The sum of all possible values of x is closest to which number?
The sum of all possible values of x is closest to which number?
5
1
8
4
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We would use here the fact that ( a m ) n = ( a n ) m = a m n and a l o g a m = m . Given that ---->
4 lo g 1 6 ( 4 x 2 − 1 2 x + 9 ) = ( 3 3 ) lo g 3 1 7 ⋅ lo g 7 ( x 2 + 2 x + 1 )
On squaring both sides ---->
( 4 lo g 1 6 ( 4 x 2 − 1 2 x + 9 ) ) 2 = ( ( 3 3 ) lo g 3 1 7 ⋅ lo g 7 ( x 2 + 2 x + 1 ) ) 2
⟹ ( 4 2 ) lo g 1 6 ( 4 x 2 − 1 2 x + 9 ) = ( ( 3 3 ) 2 ) lo g 3 1 7 ⋅ lo g 7 ( x 2 + 2 x + 1 )
⟹ 1 6 lo g 1 6 ( 4 x 2 − 1 2 x + 9 ) = ( 9 3 ) lo g 3 1 7 ⋅ lo g 7 ( x 2 + 2 x + 1 )
⟹ 1 6 lo g 1 6 ( 4 x 2 − 1 2 x + 9 ) = ( 3 1 ) lo g 3 1 7 ⋅ lo g 7 ( x 2 + 2 x + 1 )
⟹ 4 x 2 − 1 2 x + 9 = ( ( 3 1 ) lo g 3 1 7 ) lo g 7 ( x 2 + 2 x + 1 )
⟹ 4 x 2 − 1 2 x + 9 = 7 lo g 7 ( x 2 + 2 x + 1 )
⟹ 4 x 2 − 1 2 x + 9 = x 2 + 2 x + 1
⟹ 3 x 2 − 1 4 x + 8 = 0
⟹ ( x − 4 ) ( 3 x − 2 ) = 0
⟹ x = { 4 , 3 2 }
Sum of the solutions = 4 + 3 2 = 3 1 4 ≈ 4 . 6 7
Since 4 . 6 7 is closest to 5 , so 5 is our required answer.