Another russianal limit

$\displaystyle\lim_{x\to 1}\frac{x^{2015}-1}{x-1}=\displaystyle\lim_{x\to 1}\frac{(x-1)(x^{2014}+x^{2013}+x^{2012}+...+x^{2}+x+1)}{x-1}=2015$

We can apply L'Hôpital's rule which states $\large \lim _{ x\rightarrow c }{ \frac { f\left( x \right) }{ g\left( x \right) } } =\lim _{ x\rightarrow c }{ \frac { f^{ ' }\left( x \right) }{ g^{ ' }\left( x \right) } }$

$\large \lim _{ x\rightarrow 1 }{ \frac { { x }^{ 2015 }-1 }{ x-1 } } =\lim _{ x\rightarrow 1 }{ \frac { 2015{ x }^{ 2014 } }{ 1 } } =\color{#20A900}{\boxed{2015}}$

We simply use the property:

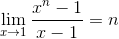
There is an elementary proof for this as well by taking $x$ $=$ $1+h$ where $h$ is infinitesimally small.Then the expression changes to $\frac{(1+h)^n - 1}{h}$ (we converted it from $x$ to $h$ ).We can expand numerator using Binomial Expansion.After expanding we cancel out $h$ from numerator and denominator.The final result is 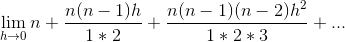But since $h$ tends to $0$ the limit reduces to $n$ .

$Q.E.D.$

lim x→1 (x^2015-1)/(x-1) =lim x→1 d/dx(x^2015-1)/d/dx(x-1) =lim x→1 2015x/1=2015

We know, Lim (x^n-a^n)/(x-a)=n a^(n-1) [as x->a] So,the answer would be 2015 (1)^2014=2015