Another sequel to the Odd Sangaku Problem by Michael Huang.
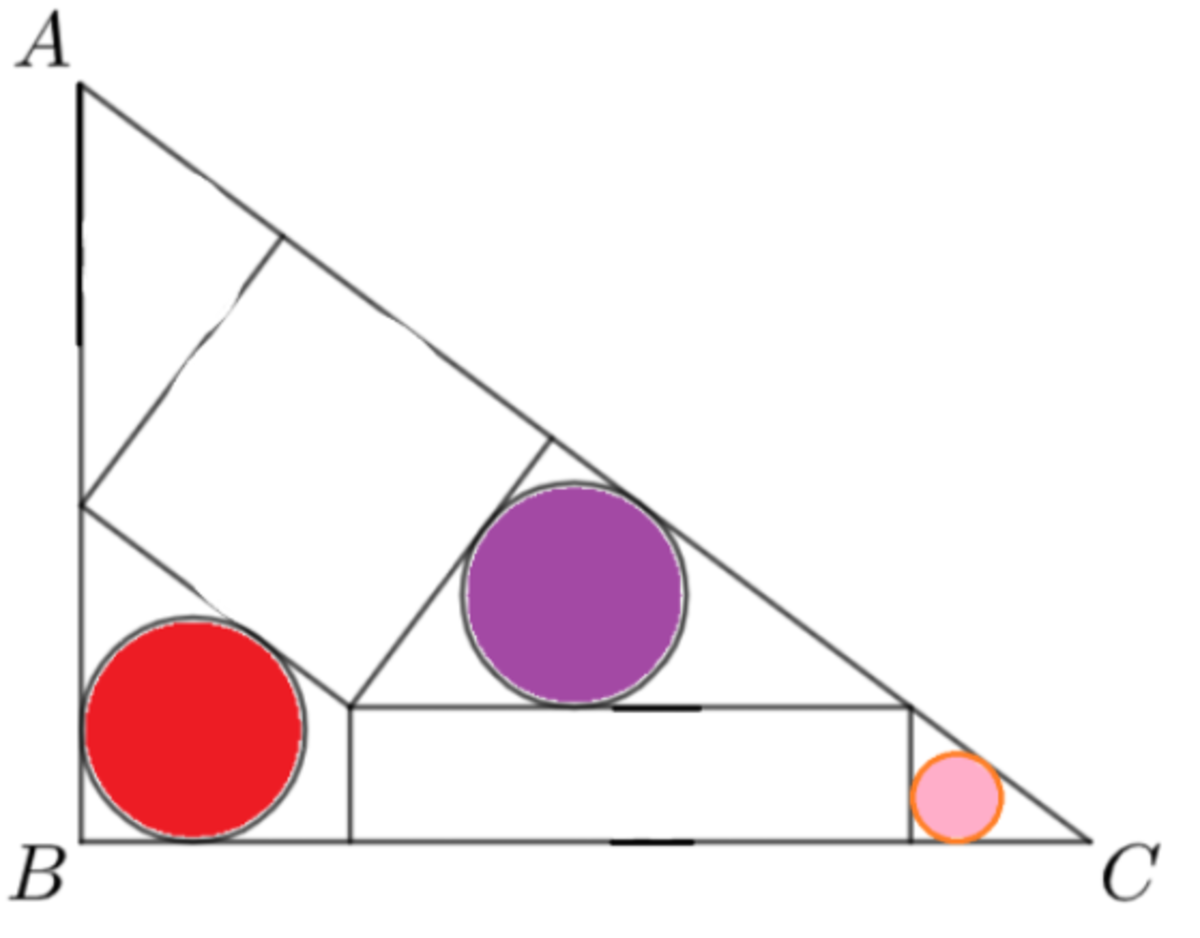
In the right triangle ABC shown in the figure above having side lengths:
AB = 27 and BC = 36
The square and the rectangle are positioned inside this triangle, such that the purple and red circles have the same radii.
Input the the square of the radius of the pink circle shown in the figure as your answer.
The answer is 2.56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the diagram as follows, add segments H F and F K , and let x = D E = E F = F G = G D .
By the Pythagorean Theorem on △ A B C , A C = 2 7 2 + 3 6 2 = 4 5 .
All the triangles are similar to each other by AA similarity, and since the purple and red circles have the same radii, △ E B K ≅ △ F G I , so E B = x .
Since △ A B C ∼ △ A D E , A E = E D ⋅ B C A C = x ⋅ 3 6 4 5 = 4 5 x .
Then A B = A E + E B = 4 5 x + x = 2 7 , which solves to x = 1 2 .
Since △ E H F ∼ △ A B C , E H = E F ⋅ A C A B = 1 2 ⋅ 4 5 2 7 = 5 3 6 .
Then I L = H B = E B − E H = 1 2 − 5 3 6 = 5 2 4 .
Since △ I L C ∼ △ A B C , L C = I L ⋅ A B B C = 5 2 4 ⋅ 2 7 3 6 = 5 3 2 and I C = I L ⋅ A B A C = 5 2 4 ⋅ 2 7 4 5 = 8 .
Therefore, the radius of the pink circle is r = 2 1 ( I L + L C − I C ) = 2 1 ( 5 2 4 + 5 3 2 − 8 ) = 5 8 , and its square is r 2 = 5 2 8 2 = 2 5 6 4 = 2 . 5 6 .