Another spring problem

Classical Mechanics Level 3

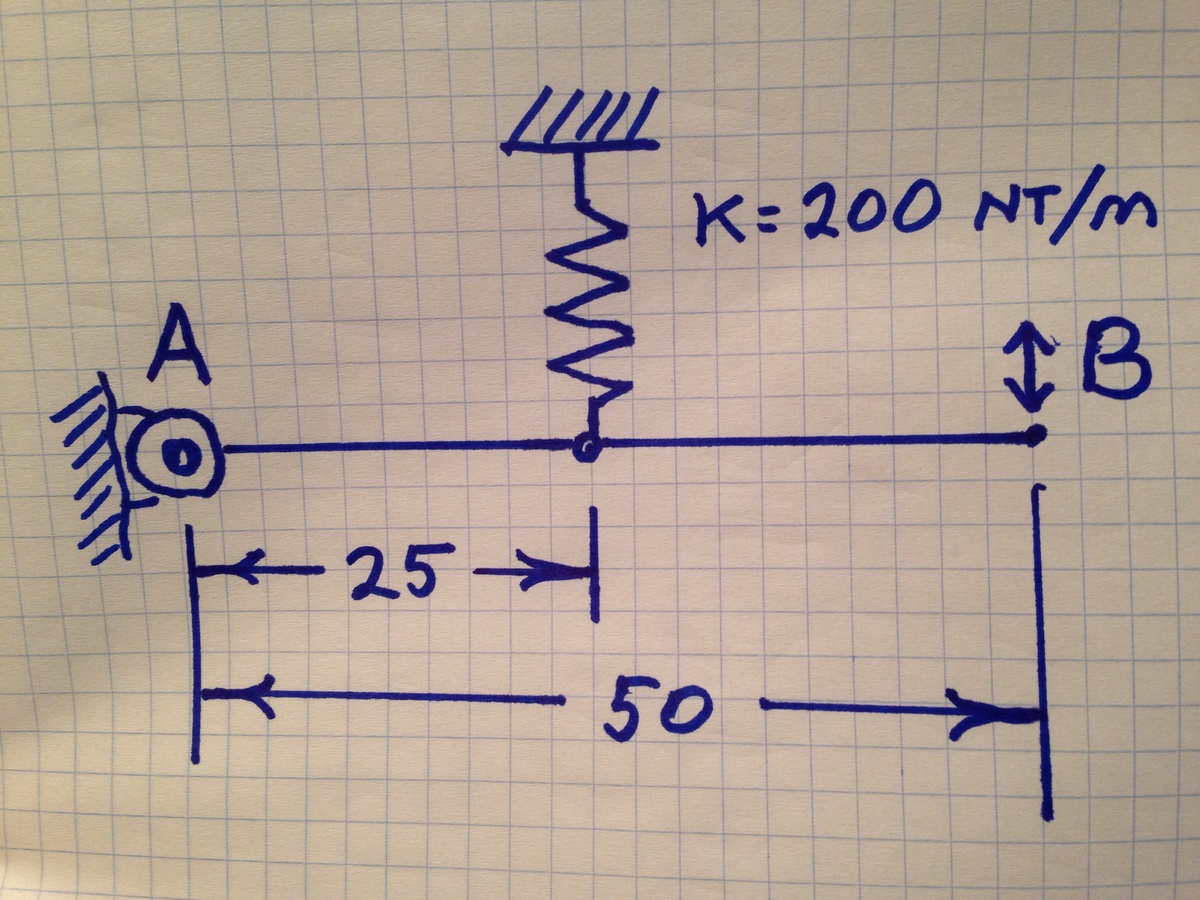
In the diagram, there is a rigid link AB of length $50\text{ cm}$ . It is attached to a frictionless bearing at point A. It can rotate about the bearing in the plane of the picture. The bearing is mounted on a rigid surface. A spring of spring constant $k = 200 \text{ Nt / M}$ is attached to link AB at a point $25\text{ cm}$ from bearing A. The spring is perpendicular to link AB, and its other end is anchored to a rigid surface. What is the effective spring constant at point B? (In $\text{Nt/M}$ )?

200 50 25 100 400

1 solution

Aniket Sanghi
Aug 16, 2016

I did it like this - ( Using SHM concepts )

Turn the rod clockwise by angle $\theta <<< \pi$ .

Then the Torque applied by the spring is

$\tau = r × F = l × kx = l × k ( l \theta )$ ,

where l is the distance of spring from A . And since $x <<< 1$ it can be treated as an arc of circle and hence $x = l × \theta$

Now equate the case when spring with spring constant 200 N/m at 25 cm and when spring with spring constant K at 50 cm .

$( 0.25)^2 × 200 × \theta = (0.5)^2 × K × \theta$

On solving we get $\boxed{K = 50N/m }$

Another spring problem

1 solution

0 pending reports