Another Summation (Part 2)

Algebra Level 4

$\large \displaystyle \sum_{m=1}^{\infty} \dfrac{m^2}{2^m}$

The summation above is equal to $\dfrac{a}{b} + c$ , where $a,b,c$ are integers, with $a$ and $b$ positive and $\text{gcd}(a,b) = 1$ , and $0 \leq c <1$ . Find $a+b-c$ .

P.S. Don't get tricked!

Try another problem on my set Let's Practice

The answer is 7.

2 solutions

Chew-Seong Cheong
Apr 24, 2017

We know that for $-1 < x < 1$ :

$\begin{aligned} \sum_{m=0}^\infty x^m & = \frac 1{1-x} & \small \color{#3D99F6} \text{Differentiating both sides w.r.t. }x \\ \sum_{m=1}^\infty m x ^{m-1} & = \frac 1{(1-x)^2} & \small \color{#3D99F6} \text{Multiplying both sides by }x \\ \sum_{m=1}^\infty m x ^m & = \frac x{(1-x)^2} & \small \color{#3D99F6} \text{Differentiating both sides w.r.t. }x \\ \sum_{m=1}^\infty m^2 x ^{m-1} & = \frac {1+x}{(1-x)^3} & \small \color{#3D99F6} \text{Multiplying both sides by }x \\ \sum_{m=1}^\infty m^2 x^m & = \frac {x(1+x)}{(1-x)^3} & \small \color{#3D99F6} \text{Putting }x = \frac 12 \\ \implies \sum_{m=1}^\infty \frac {m^2}{2^m} & = \frac {\frac 12 \cdot \frac 32}{\frac 18} = 6 \end{aligned}$

$\implies a+b-c = 6+1-0 = \boxed{7}$

Upon diffrentation in the second line.... shouldn't it be negAtive?

Sid Patak - 3 years, 12 months ago

Never mind sorry... ill delete this comment

Sid Patak - 3 years, 12 months ago

Zach Abueg
Apr 22, 2017

Let $\displaystyle \sum_{m \ = \ 1}^{\infty} \frac {m^2}{2^m} = S$ .

The series with index $m = 0$ has $\displaystyle a_0 = 0$ , so they are the same series:

$\displaystyle S = \sum_{m \ = \ 1}^{\infty} \frac {m^2}{2^m} = \sum_{m \ = \ 0}^{\infty} \frac {m^2}{2^m}$

We also know that we can manipulate the index if we change $n^{th}$ term:

$\displaystyle S = \sum_{m \ = \ 1}^{\infty} \frac {m^2}{2^m} = \sum_{m \ = \ 0}^{\infty} \frac {(m + 1)^2}{2^{m + 1}}$

Thus,

$\displaystyle S = \sum_{m \ = \ 0}^{\infty} \frac {m^2}{2^m} = \sum_{m \ = \ 0}^{\infty} \frac {(m + 1)^2}{2^{m + 1}}$

Now let's do some rewriting:

$\displaystyle S = 2S - S$

$\displaystyle = \sum_{m \ = \ 0}^{\infty} \frac {(m + 1)^2}{2^m} - \sum_{m \ = \ 0}^{\infty} \frac {m^2}{2^m}$

$\displaystyle = \sum_{m \ = \ 0}^{\infty} \frac {2m + 1}{2^m}$

$\displaystyle = \sum_{m \ = \ 0}^{\infty} \frac {2m}{2^m} + \sum_{m \ = \ 0}^{\infty} \frac {1}{2^m}$

$\displaystyle = 2\sum_{m \ = \ 0}^{\infty} \frac {1}{2^m} + \sum_{m \ = \ 0}^{\infty} \frac {1}{2^m}$

$\displaystyle = 4 + 2 = 6$

$\displaystyle \sum_{m \ = \ 1}^{\infty} \frac {m^2}{2^m} = 6$

Since $\displaystyle 0 ≤ c < 1$ and $c$ must be an integer, $c = 0$ . $\displaystyle 6 = \frac 61$ , so $a = 6$ and $b = 1$ .

$\displaystyle a + b - c = \boxed{7}$

Nice solution, but I am a bit confused about the equality between line 4 and 5 counting from S=2S-S. What happened to m in the first term of the 4th line?

Magne Myhren - 4 years, 1 month ago

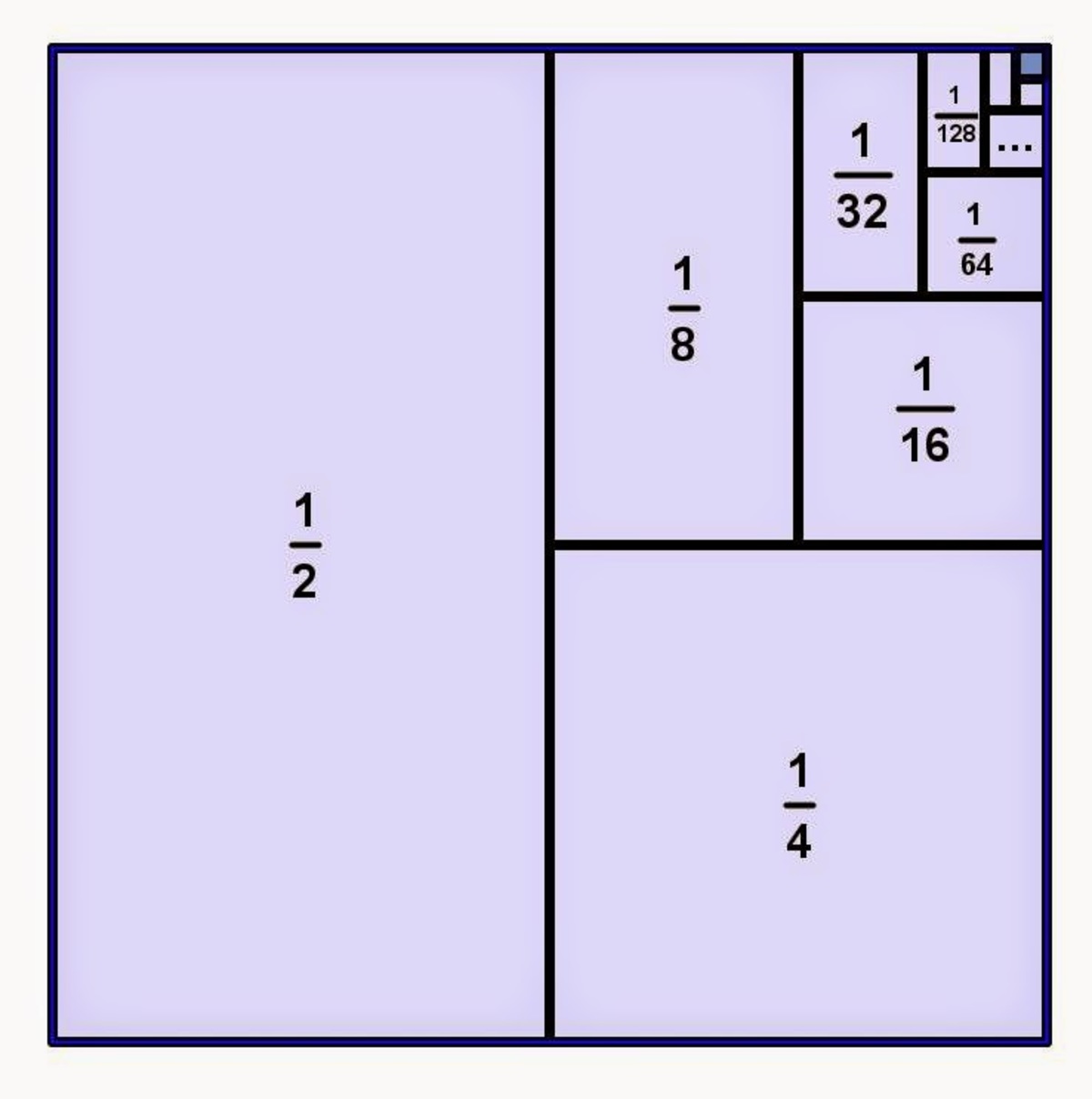
You can see by this proof without words that

$\displaystyle \sum_{m \ = \ 0}^{\infty} \frac{1}{2^m} = 2$

$\displaystyle \sum_{m \ = \ 0}^{\infty} \frac{2m}{2^m}$ is twice the sum of $\displaystyle \sum_{m \ = \ 0}^{\infty} \frac{1}{2^m}$ ; you can easily check this using partial sums.

Zach Abueg - 4 years, 1 month ago

Another Summation (Part 2)

Try another problem on my set Let's Practice

The answer is 7.

2 solutions

0 pending reports