Another useless wire!

Electricity and Magnetism Level 2

I had a useless metallic wire of total resistance $60 \Omega$ , and then I cut it into twelve equal parts and formed a regular octahedron. What is the resistance between any two opposite nodes in $\Omega$ ?

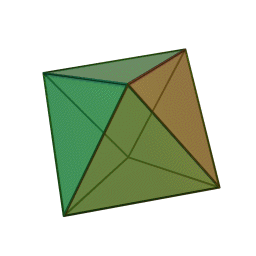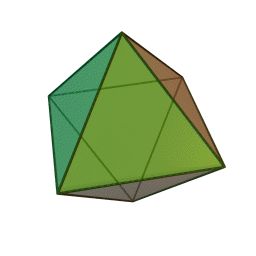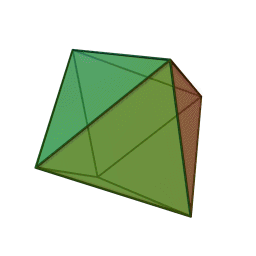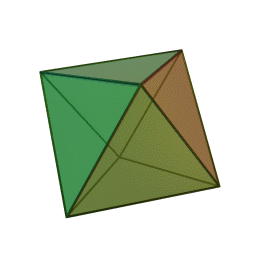
Image credit:Wikipedia

This problem is original.

This question is part of the set Platonic Electricity .

The answer is 2.5.

1 solution

Swapnil Das
Jun 4, 2016

First of all, let the octahedral circuit get stable, so that we can analyze it ;)

Now, as $R\propto l$ , each resistor has a resistance of $\frac{60}{12}=5 \Omega.$

We apply a voltage to any two opposite nodes,say $E$ and $F$ . By symmetry of the circuit, we can easily observes that points $A,B,C,D$ are equipotential with respect to nodes $E$ and $F$ . Therefore, the circuit can be redrawn to two resistors in series, each with resistance $\frac{5}{4}\Omega$ .

$\therefore$ The Equivalent resistance is $\frac{5}{2} \Omega$ .

Nice explanation (+1) solved it the same way

Ashish Menon - 5 years ago

Or it can be generalized that the resistance between any two adjacent nodes of a n-sided 3D figure is $\dfrac{\text{Resistance of wire}}{2 × \text{Number of edges}}$ .

In this question, the octahedral has $12$ edges and total resistance of wire is $60\Omega$ .
So, resistance = $\dfrac{60}{2×12} = \dfrac{5}{2} = \color{#3D99F6}{\boxed{2.5}}$ .

Ashish Menon - 5 years ago

Hmm, never knew about the formula, thanks anyways.

Do you know its proof?

Swapnil Das - 5 years ago

Nono, I dont know the proof, I just observed that a 3 sided 3D figure has x, and 4sided one y, a 5sided one z and 6 sided one w and generalized XD

Ashish Menon - 5 years ago

This is something new ;). But, Ashish, we are talking about opposite nodes. Please check it.

Abhay Tiwari - 5 years ago

sir is there formula for equivalent resistance along two opposite sides

Deepansh Jindal - 5 years ago

Another useless wire!

The answer is 2.5.

1 solution

0 pending reports