Can You Answer In One Minute Or Less?
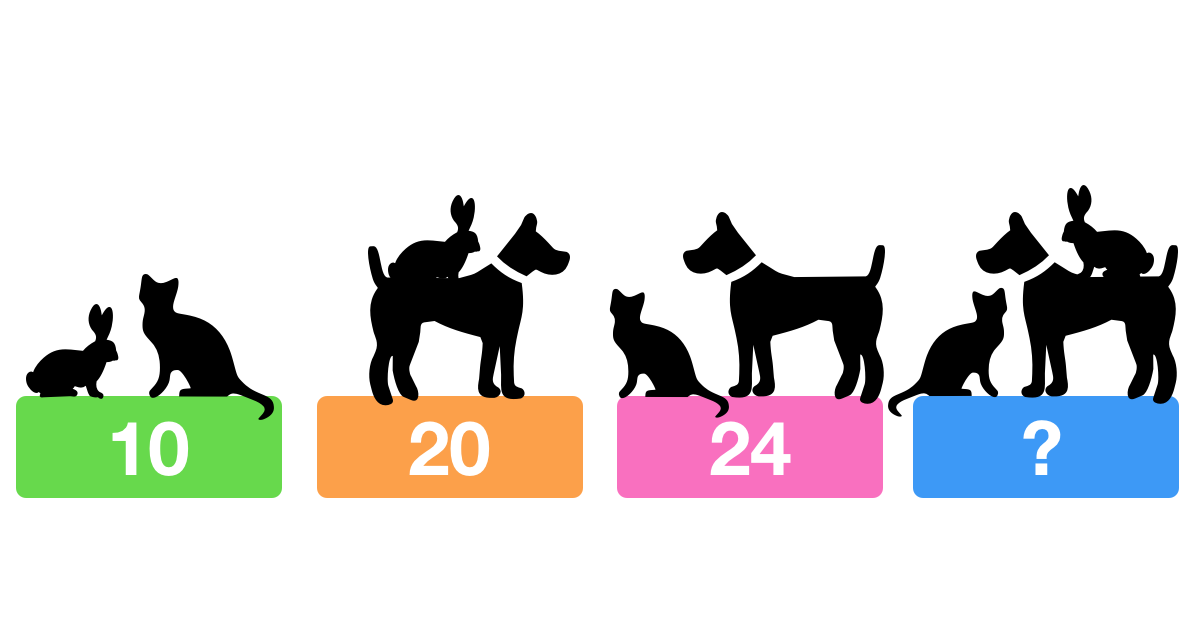
What weight will the fourth scale display?
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
Discussions for this problem are now closed
Is it bad that I just figured out which two numbers would equal 10?? 5 and 5 didn't add up. If you subtract 5 from 20 (get rid of the rabbit weight) and then add 5 to get 24 (add the cat) it doesn't work. 6 and 4 was the same way. But 3 and 7 works! Subtract 3 from 20 (to get the dog's solo weight) and then add 7 (to get the dog and cat's combined weight). Add 3, 7, and 17 to get 27! (my brain works oddly)
I also used such logic first. But it always take unnecessary time so it is better to follow the calculation.
well it was a trial and error process
Good!! Smart enough
Don't worry that's how my mind functioned ! Haha not bad, we just analyze differently.
I did the same t hing - my brain works oddly too!! ha ha
I did it that way, and still answered in less than a minute. It would have taken me longer to formulate the question in algebra, at which I am, and have always been, useless.
the difference between cat+dog and bunny+dog is four. so the cat is four more than the bunny. Therefore you need a number (x) that when added to four (x+4) gives you another number (y) that when added to the first number give you 10 So (x+4=y and x+y=10) (the bunny) x=3, (the cat) y=7 & the dog would be 17 which makes every statement true 3+7=10 , 3+17=20, 7+17=24, then you combine all three numbers and get 3+7+17=27. Kinda confusing but that's how my mind works.
add first 2 pics you get 2rabbit+cat+dog=10+20=30kg then take away 3rd pic from 30kg. you are left with 2 rabbit= 6kg so 1 rabbit =3kg add that to the 2nd pic you get 27kg
Similar to chemistry's Hess's Law
Let r, c, and d correspond to rabbit, cat, and dog. The with the system of equations, you get this: r + c = 10 d + c = 24 d + r = 20
You can add the first two equations:
2c + (r + d) = 34
Since r + d was already given in c a separate equation, you can substract it from the sum above.
2c + (r + d) - (r + d) = 34 - 20 2c = 14 c = 7
Now you can simply add it to the equation without c
(r + d) + c = 20 + 7 = 27
Yay!
x
+
y
=
1
0
y
+
z
=
2
0
z
+
x
=
2
4
Adding all three equations gives 2 ( x + y + z ) = 5 4 , so x + y + z = 2 7 .
Form some simultaneous equations: r+c=10 r+d=20 and c+d=24. Adding these together gives 2c+2r+2d=54, halving gives the weight of all three, namely 27kg.
- A = Rabbit
- B = Cat
- C = Dog
Here we turn the question into maths
A + B = 1 0
A + C = 2 0
B + C = 2 4
We then rearrange the first two equations to give us A on one side
A = 1 0 − B
A = 2 0 − C
Make them equal each other
1 0 − B = 2 0 − C
We then arrange the equation so that variables and numbers are on different sides - then work through
C − B = 1 0
B = C − 1 0
B = 2 4 − C
Here we use the the first equation to compare against
C − 1 0 = 2 4 − C
2 C = 3 4
C = 1 7
Now we just substitute for A and B
A + C = 2 0
A + 1 7 = 2 0
A = 3
A + B = 1 0
3 + B = 1 0
B = 7
A = 3
B = 7
C = 1 7
Add them together...
A + B + C = 2 7
At first, I was thinking you'd solve this mathematically where you create three equations with 3 variables and solve fore each with substitution. Then I realized it'd be easier to add all the total weights and divide by 2 since that weight is the weight of 2 of each animal.
Same here.
I used more logic than actual math workout for this one:
By comparing the weight between D + C (24) and D + B (20), I knew that C = B + 4. Then I rewrote C + B = 10 into 2B + 4 =10, solving for B (3). Finally, I added B to C + D in order to get C + D + B (24 + 3 = 27).
a+b=10, b+c=20, a+c=24; b=10-a, c=24-a; 10-a+24-a=20, a=7; 7+b=10, b=3; 3+c=20, c=17; a+b+c=27.
let we name these 3 animal x=cat, y=rabbit,z=dog
X+Y=10.....................................(1)
Y+Z=20.....................................(2)
Z+X=24......................................(3)
then X+Y+Z=? let, X+Y=10 then X=10-Y substitute this in eqn3 Z+X=24 Z+(10-Y)=24 Z-Y=24+10=14 eqn2, Y+Z=20 -Y+Z=14 cancel y and we get 2Z=34 then Z=17 substitute Z=17 in eqn2 Y+17=20 then, Y=3 we found that Y=3, Z=17 substitute Y=3 in eqn1 X+3=10 then X=7 then X=7 Y=3 Z=17 X+Y+Z=27
You have found the weights of all three animals, however it's not necessary. Since the problem only asks for the sum of x + y + z , it would have been easier to add the equations and then divide it by 2.
Add the all the given weights to get 54. This means that two of each on a scale weighs 54 kg, and divide by 2 to get that one of each on the scale weighs 27 kg
Nice solution!
C + R = 10 D + R = 20 C +D = 24
double the middle equation: 2D + 2R = 40 Add the first equation: C + R = 10 Subtract 3rd equation also: -C -D = -24
These get you D + 3R = 26 subtract 2nd equation -D - R = 20
Therefore 2R = 6 and R=3
From there c = 7 and d = 17 and the grand total is 27! QED
by implementing each animal as variables....we observe: figure 1:x+y=10 figure 2:y+z=20 figure 3:x+z=24 solving the above equations, we get: x=7 y=3 z=17 in the last figure,we observe,x+y+z=? and its 27
2 dog+2 cat+2*rabit=54
2(dog+cat+rabit)=54
dog+cat+rabit=27
keep it simple just see all the animals come twice; so divide the addition of all by 2 therefore [20+10+24] /2 =27!!!
Assume the cat weighs 7kg and therefore the rabbit is 3kg in scale number 1, hence in scale number 2 the dog is 17kg because the rabbit is 3kg. In scale number 3, the dog which is 17kg plus the cat which was assumed at 7kg totals 24kg putting their sum at scale number 4 to 27kg over all because the cat is 7kg, the rabbit is 3kg and the dog is 17kg!
There 3 animals in the picture - cat, rabbit, and dog Let c = cat r = rabbit d = dog
Now let's write a system of equations according to the scales c + r = 10 d + r = 20 c + d = 24
When we subtract c + r = 10 and d + r = 20, we get d - c =24 When we subtract d - c =24 from the 3rd equation we get 2d = 34 So d = 17 So you can plug d = 17 into the other equations, and you done!
c=cat
r=rabbit
d=dog
Now for the maths:
c+r=10
d+r=20
c+d=24
To work it out:
24-20=4
Which means:
Therefore c=r+4
So:
c+r=2r+4=10
10-4=6
6/2=3
We now know that r=3
And from that we can figure out:
10-3 =7 so c=7
20-3=17 so d=17
so the answer is:
c+d+r=3+7+17=27
Moderator note:
Thanks for defining your terms clearly at the start. That makes it easier to understand what you are saying.
You can improve the writeup by explaining what you are doing. For example, instead of saying
24-20=4
Which means:
Therefore c=r+4
you should write it as " c − r = ( c + d ) − ( r + d ) = 2 4 − 2 0 = 4 . Hence c = r + 4 ". This makes it much clearer for someone else to understand how " 2 4 − 2 0 = 4 means that c = r + 4 ".
Since the three animals has different weights and appears at least 3 times (including the 4th scale!), I will start with the first scale.
Labels:
c-cat
r-rabbit
d-dog
7+3=10 (c+r)
17+3=20 (d+r)
7+17=24 (c+d)
And we know the cat is 7 kg, the dog is 17 kg and the rabbit is 3 kg. Now add it up.
17+7+3=27
So the total weight of the animals is 27 kg.
Even simpler, each animal is on two scales. This means that the weight of each animal is counted twice. If you add up all the known weights, you get 54 kg. This is two bunnies, two cats, and two dogs. To find the mass of just one, divide by two and you get 27 kg.
10+20+24 = 54
54/2 = 27 --> Answer
Here's what I did:
1.) Add the Dog and the Bunnys weight (20kg) to the Dog and the cat's weight (24kg) to get 44. So far you've counted the dog twice, the bunny once and the cat once.
2.) I'm trying to get the dog weight by itself so next I subtract the cat and the bunny weight (10kg) from 44. You get 34 but this number represents having counted the dog twice. So we divide by 2 to get 17. Now we have the dogs weight alone.
3.) 17 + 10 = 27
add first two scales 10+20=30=1cat+1dog+2rabbits given 1dog+1cat=24; subtract we get 6=weight of two rabbits...so add 3 to 24(weight of cat nd dog) WE CAN CALCULATE IN OUR MIND BY THIS METHOD.
x = cat y = rabbit z = dog
x+y = 10 x+z = 24 z+y = 20
required : x+y+z = ?
substitute the following equations
x + y + 0 = 10 x + 0 + z = 24 0 + y + z = 20
solve for x+z first
(x + y + 0 = 10) - 1 0 + y + z = 20
-x - y + 0 = -10 0 + y + z = 20 cancel out y
new equation is
-x +z = 10 x + z = 24
2z = 34
z = 17
y = 20 - 17
y = 3
x = 24 - 17
x = 7 x + y +z = 17 + 3 + 7
answer = 27
If B+D =20 and C+D =24. Then C = B+4. Therefore if B = X, then C = X+4.
X+X+4 = 10.
2X+4 =10.
2X =6.
X= 3.
C = 3+4 =7.
D+3 = 20. D = 17.
B+C+D = 3+7+17 = 27
Moderator note:
Good clear explanation.
Can you find an alternative solution that doesn't require you to solve for all of the individual values?

Relevant wiki: System of Equations - Substitution
Let R = weight of the rabbit, D = weight of the dog, and C = weight of the cat. The pictures then give us the following equations: R + C = 1 0 R + D = 2 0 C + D = 2 4 If we add all three equations, we obtain 2 R + 2 C + 2 D = 5 4 ⟶ R + C + D = 2 7 .