Ant-omology

Geometry Level pending

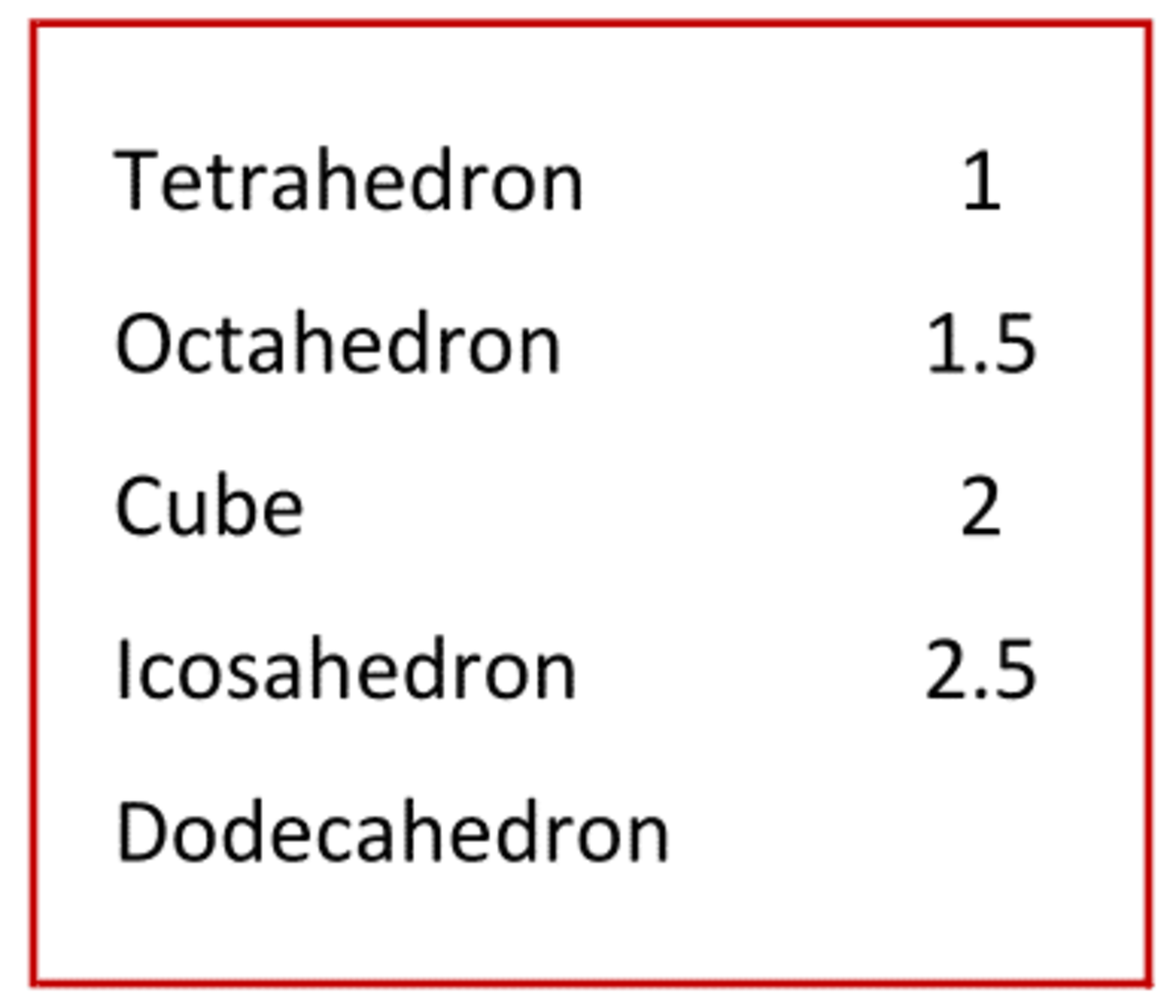A hardworking ant has figured the shortest distance along the surface between the midpoints of two opposing edges for the first four unit Platonic solids but needs some help with the dodecahedron.

Details:

  • The solid is a regular dodecahedron with edge size 1.

  • The points to connect are midpoints of their respective edges and are opposite each other, that is a straight line connecting them goes through the center of the solid.

  • The shortest distance is to be measured along the surface of the dodecahedron.

  • Give your answer to three decimal places.


The answer is 3.927.

Marta Reece by Marta Reece , 69, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Marta Reece
Apr 28, 2017

The yellow line is shorter than the red, so that’s the one pictured below. The line is made of three equal segments. Each of those is equal to 1 plus the projection of 1 2 \frac{1}{2} into the direction. The angle for the projection is the internal angle of a pentagon minus 9 0 ∘ 90^\circ , that is 10 8 ∘ − 9 0 ∘ = 1 8 ∘ 108^\circ-90^\circ=18^\circ .

Each segment: 1 + 2 × 1 2 sin ⁡ 1 8 ∘ = 3 + 5 4 1+2\times\frac{1}{2}\sin18^\circ=\frac{3+\sqrt{5}}{4}

The entire distance: 3 × 3 + 5 4 ≈ 3.927 3\times\frac{3+\sqrt{5}}{4}\approx\boxed{3.927}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...