Ant on a large die

Geometry Level 5

An ant begins at a point P on one edge of an ordinary, but large, cubical die. He visits all 6 faces of the die in the following order: 5, 3, 1, 4, 2, 6, at which point he has returned to P. He takes the shortest possible route for this particular journey, walking 5cm, 10cm, 15cm, 5cm, 10cm, and 15cm respectively on each face.

Find the surface area of the die in cm $^2$ .

Note: The opposite faces on an ordinary die add up to 7.

The answer is 1080.

2 solutions

Paul Hindess
Dec 15, 2016

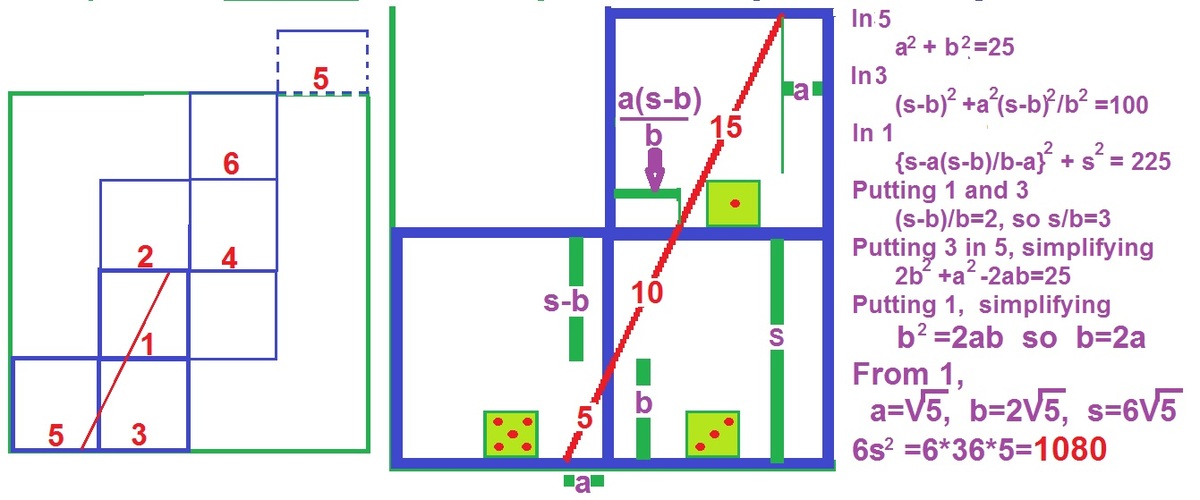
The black arrow on the diagram shows the ant's journey. The key thing is that although this is the shortest route to visit all the faces in the order specified, it is not the shortest route to visit all the faces (that would be in the order 5, 3, 1, 2, 4, 6 or similar).

Notice that the ant walks 15cm across the "1" face. This length has been translated to create the hypotenuse of a right-angled triangle where $s$ is the side length of the cube.

By Pythagoras' Theorem, we have $s^2 + (\frac12s)^2 = 15^2$ which leads to $s^2 = 180$ .

Now $s^2$ is the area of one face of the cube, so the surface area of the cube = $6s^2 = 180 \times 6 = 1080$ cm $^2$ .

So the answer is 1080.

Beautiful solution. +1)

Niranjan Khanderia - 4 years, 5 months ago

Niranjan Khanderia
Dec 21, 2016

Solution by Paul Hindess is much better. But just to give another approach.

Thanks for posting! I thought up the problem when running my fingers around a Rubik's cube (other rotating puzzle cubes are available!). I was trying to come up with a problem involving a slice being taken through a cube at an unusual angle, but never came up with anything satisfactory. This problem was a byproduct.

I did so many awful calculations before I posted the problem that I ended up learning a lot from a whole host of errors. Had I not had that experience, I'm sure my solution would have been far more convoluted.

Paul Hindess - 4 years, 5 months ago

Ant on a large die

The answer is 1080.

2 solutions

0 pending reports