Ant on a Triangular Grid
If an ant starts on a vertex of a grid composed of equilateral triangles (whose bases run east and west) and crawls the shortest route to a point that is 8 triangle bases east and 4 triangle heights north of its starting point, then it will pass through 16 equilateral triangles:
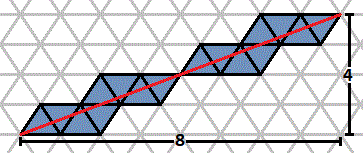
Find the number of triangles an ant will pass through if it crawls the shortest route to a point that is 1000 triangle bases east and 550 triangle heights north of its starting point instead.
The answer is 2500.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I got 2400.... not by ths method, this is a good method
The ant enters a new triangle every time it crosses a line. Things are trickier if the ant's path hits an intersection in the grid - but we get around that by splitting the path up at these points. The ant first hits an intersection after crawling 4 0 triangles east and 2 2 triangles north (bonus question: why not 2 0 triangles east and 1 1 triangles north?). During this journey, it crosses 2 1 east-west lines, 3 9 NW-SE (ish) lines, and 4 0 SW-NE (ish) lines, entering a total of 2 1 + 3 9 + 4 0 = 1 0 0 triangles on its way. It then repeats this path 2 4 more times, for a total of 2 5 × 1 0 0 = 2 5 0 0 triangles along its path.
Why not 22??
Really nice solution! One comment: The ant crosses many more NW-SE lines than SW-NE lines. In the picture provided for the 8 × 4 grid, you can count 1 0 of the first type and 6 of the second type (perhaps adjusting slightly for the starting and ending points).
For the 4 0 × 2 2 grid example, there are 4 0 + 2 2 / 2 = 5 1 NW-SE lines and 4 0 − 2 2 / 2 = 2 9 SW-NE lines, rather than 4 0 of each. So the count is more like 2 1 + 5 0 + 2 9 = 1 0 0 than 2 1 + 3 9 + 4 0 = 1 0 0 .
On a square grid, an ant that crawls x units east and y units north for relatively prime x and y will pass through a total of 1 starting square (colored gray below), x − 1 squares to the right of each vertical intersection (colored blue below), and y − 1 squares above each horizontal intersection (colored green below) for a total of S = 1 + ( x − 1 ) + ( y − 1 ) = x + y − 1 squares.
If x and y are not relatively prime, the diagram can be split up into g cd ( x , y ) identical g cd ( x , y ) x × g cd ( x , y ) y rectangles.
Applying the above equation, the number of squares the ant would pass through is S = g cd ( x , y ) × ( g cd ( x , y ) x + g cd ( x , y ) y − 1 ) or
S = x + y − g cd ( x , y )
A equilateral triangular grid can be transformed into a square grid, where each square is 2 triangles, and the number of triangular bases east is reduced to x − 2 1 y squares east.
Substituting x − 2 1 y and y into the equation above and multiplying it by 2 , the number of triangles that ant would pass through is T = 2 ( ( x − 2 1 y ) + y − g cd ( x − 2 1 y , y ) ) or
T = 2 x + y − 2 ⋅ g cd ( x − 2 1 y , y )
Therefore, for x = 1 0 0 0 and y = 5 5 0 , the ant would pass through T = 2 ⋅ 1 0 0 0 + 5 5 0 − 2 ⋅ g cd ( 1 0 0 0 − 2 1 ⋅ 5 5 0 , 5 5 0 ) = 2 5 0 0 triangles.