Ants assembly
Six ants are sitting at the six vertices of a hexagon, The ants start moving randomly towards one of the neighbor vertices and then stop. The probability that at least three ants will meet at the center of the hexagon can be expressed as , where and are coprime positive integers, find .
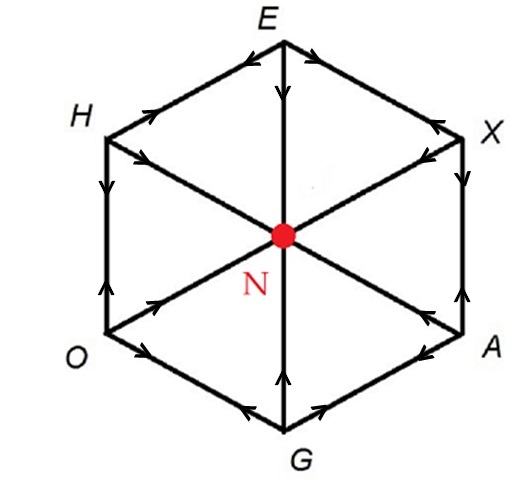
The answer is 962.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The probability of exactly 0 ≤ n ≤ 6 ants meeting at the center is
p ( n ) = ( 3 1 ) n ⋅ ( 3 2 ) 6 − n ⋅ ( n 6 )
This is because the probability of exactly n specific ants moving to the center is ( 3 1 ) n , the probability of the other 6 − n ants moving somewhere else is ( 3 2 ) 6 − n , and finally there are ( n 6 ) ways to choose n specific ants.
Now, we only have to add up all probabilities
p ( 3 ) + p ( 4 ) + p ( 5 ) + p ( 6 ) = 7 2 9 2 3 3
and so the answer is 2 3 3 + 7 2 9 = 9 6 2 .