An Ant's path
An ant is crawling along the surface of a cylinder with a diameter and a height. What is the shortest path he can crawl from point to point ? Give your answer to 3 decimal places.
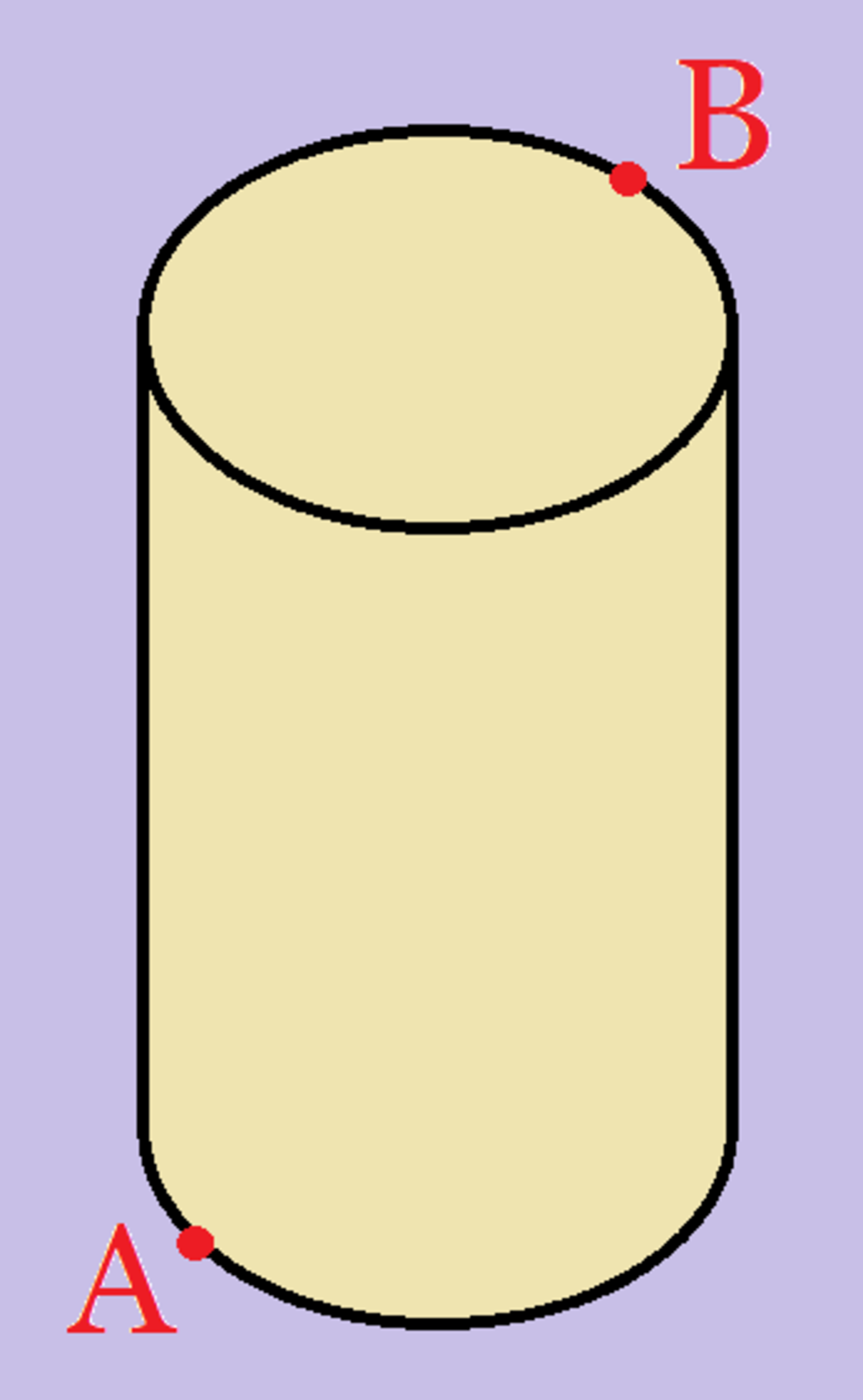
Clarification: point is on the edge of the base and point is on the edge of the top of the cylinder on the side.
The answer is 7.448.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are two cases and we need to compare which one gives us the minimum value.
Case 1: Ant travels from A along the height and the diameter to reach B. In this case, the distance travelled is 4 + 4 = 8 cm.
Case 2: Ant travels from A along the curved surface to reach B. Since A and B are on the opposite side, we can visualize by cutting open the cylinder.
When you cut a cylinder along its height, it forms a rectangle of breadth h and length 2 π r. If you cut along the plane of A, you will observe that B is at the mid-point of this rectangle, thus forming a right angled triangle. We need to find the length of AB that is a line joining the mid-point of the length of the rectangle from point A.
So using pythagoras theorem, we get AB = ( 4 2 + ( 2 π ) 2 ) = 7.448 cm