Pressure Difference At The Bottom Of The Cup
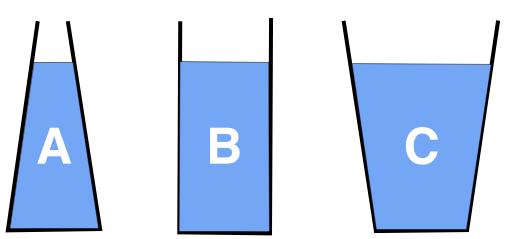Which of the following choices has the highest water pressure at the bottom of the container?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
The pressure in any of the vessels comes from the atmosphere, and gravity's downward pull. Fluids can't maintain a net force in any given direction (if there were such a force, the fluid would rearrange to relieve it), and so at any depth, the pressure is uniform.
This means that for any vertical column of water, the pressure at any height can only be due to the atmosphere and gravity's effect on that column of water. Any column that's above the slanted walls in the vessel on the left is supported by the wall of the vessel, and the columns above the base are supported by the base. We can make any sort of shape we like, but at the circular base, the pressure depends only on the height of the water column.
Note this also means that the column above the bass need not even be continuous, i.e. the vessel could have an hour-glass shape, and the pressure on the base would remain the same.
Isn't container C more heavy than the rest of the container because it has more Water. So the pressure should be higher at the bottom if the bottom has the same area as the other container.
Log in to reply
Take a look at the side walls of container. They are tilted outside.Some of the y-component of Force acts on these walls too. The water in the centre only is responsible for putting pressure. Here density and height counts, not the mass.
https://www.youtube.com/watch?v=J7ymn6f2Bl8
Log in to reply
Hydrostatic pressure only applies if there is an object in the water. If it is exerting force on the bottom, the density of mass over surface area is relevant.
not true because the main law is pressure = force/ area . pressure = volume x p x g / area of the bottom , volume of cylinder is area x height but the volume of this shape is equal medium base x height and it is not equal to the area of base ,so we can use the law pressure = h x p x g only if the shape is cylinder or if the volume is so big as sea but in this case the shape make difference do the greatest pressure in case "c"
Log in to reply
I agree, draw vectors and you will see the answer.
this is correct, if the main factors are force and area, problem says identical force hence that equation applies
Force from a larger area can transfer to a smaller area.
The weight of the liquid in the container is equal to Vpg. As explained above by the moderator, the pressure at the base doesn't depend on the weight of the liquid it carries.
But it said at the bottom
Your question is misleading. It should be "Which of the following choices has higher water pressure in at the bottom of the container?" and NOT "Which of the following choices has higher pressure in the bottom?" Because readers, like me, might think you meant the pressure exerted by the base of the container on the surface it is positioned on and not the water pressure itself. They might use P = m x g/A instead of P = h x (m/v) x g = h x d x g, where P is pressure calculated, m is the mass of the object exerting the pressure, g is the gravitational constant of acceleration, A is the area of the object exerting the pressure that is in contact with the surface that is receiving the pressure, h is the maximum height reached by the water in the container object, d is the density of water and v is the volume of water inside the container.
Log in to reply
Sorry man ,my bad.
Thank you. Some one points out why the wording of this question is what's messing people up. I used the same logic as you.
Well all those calculation if we take for granded that all containers have the same area at the bottom, since the pressure depends only from height, since the have the same fluid, all three containers have the same pressure. However force=pressure/area. The forces are equal only in case the containers have the same area.
Log in to reply
Whoa there, force = pressure * area. But yes, I see your point.
Imagine two identical containers, for example cylinders, with height h and bottom area A, so that the volume of both containers equals Ah. Container 1 is filled completely with water, but container 2 has a rock in it, that is held up by a few rods that are connected to the inner wall of the container. Let's assume that the rock occupies 90% of the volume of container 2, but doesn't touch the bottom or the sides, so that the water can freely fill the surroundings of the rock within the container, in such a way that all the volume Ah is taken by the water plus the rock. Does this still mean that the pressure on the bottom of both containers is equal? That doesn't seem to make sense.
What about the normal reaction's components in the downward direction due to the side of the walls? The areas of the base look similar so that should add up in (a) nothing in (b) and get subtracted in (c)
The force due to side wall in the downward direction is also in 1st picture,it is cancelled in the middle one and force due to side walls in the upward direction is in the 3rd picture.This can be easily seen during the force balance.
Webster is wrong or ya are, Def: the (WEIGHT) or force that is produced when something presses or pushes against something else. We know "c" has the most weight!
h = volume/area. If all h and area are the same then the volume are varied. Pressure = volume x density x gravity / area. Therefore the pressure is veried on its volume. Which is depended on the container shape.
Why is it paradox?... If I consider two different vessel of same height but different base area then the amount of liquid varies as they have different volume. But as the hydrostatic force on an object immerge inside a liquid is symmetric, hence the pressure at the bottom of the vessel is only due to vertical portion above the base.....
the issue, i see, is controversial.. can we see an experiment that show this law?
"C" has a greater volume of water acting on a given area. So the force on the bottom of the container should be greater. The wording could be better on this problem by using proper terms lime static fluid pressure etc. It is slightly unclear what they are asking.
Understanding what has been said about the pressure bein related to the height of the water, I don't see how container A would have the same pressure across the entire bottom since the walls taper inward. Wouldn't the pressure only be the same as the other containers in the very center where there are no walls above it, and then less as you move outward?
It's due to the shape, their volumes are different and so, their capacity is different as well. Considering that a unit volume of water has mass m, all the different containers will have a different amount of water. We also know that pressure = Thrust/Area And the thrust applied will be more for the last container, since it visually has more volume. And that force in this case is mg. Therefore the pressure should be the highest in the third container.
That will only be true if the volume were the same in each vessel witch it appear to not be
you misspelled base
I thought it said the pressure on the vessel's bottom itself.
What about the pressure of the ocean depending on depth?
This makes a consideration for which structure to choose for my drinkings.
AT SAME HIGHT SAME PRESSURE IN SAME FLUID.PRESSURE CHANGE IF WE GOES UP OR DOWNIN SAME FLUID. CHANGE IN PRESSURE ENERGY=-Z Z=IF WE GO DOWN THAN TAKE + IVE CHANGE. AND IF WE GO UP THAN TAKE -IVE SIGN.
Some spell check is in order!
Log in to reply
Maybe English isn't Gp Dhaker's first language. I don't think his spelling undermines his intelligence at all.
Log in to reply
It's difficult to understand what he is trying to explain. You can't teach someone something if you can't explain it well....
The pressure at the bottom of the container is equal to the height from the water surface to the bottom of the container multiplied by the unit weight of water. Since the heights are equal and the unit weight of water are equal, the pressures at the bottom of the containers are also equal.
What if the question was- which container has the greatest psi ? Would the answer then be “C” ?
I was a little confused because of the shape of the glassware whether the question was really asking for pressure or psi.
Log in to reply
Isn't the pressure measured in Pounds/Square/Inch?
All you are doing is repeating a law... not TESTING or EXPLAINING the law. One has to explain the law... for even incorrect "laws" can be repeated.
Here is a thought problem for you to consider.
Imagine there is a diver in a 10' diameter cylinder, filled to 10' height... even though the cylindrical container goes up one mile.
Now imagine there is another container next to it shaped like a cone, with a 10' base... but it quickly narrows leaving just enough room for a diver... the top of the cone stops at about 5', and NEARLY closes.... from there a very small pipette extends upward a mile + 5' (matching the height of the cylinder next to it).
We now add water to both containers... all the way to the mile mark.
The diver in the cylinder is crushed and dies.
The other container with the extremely thin neck is filled to the one mile mark with only 1 gallon of water.
Discounting any surface tension effects, etc... will the addition of this 1 gallon of water crush the diver the same as the first?
What explains the massive crushing force behind 1 gallon of water?
A pic is worth a thousand words .if I could imagine it in real life for relation SAKE .I guess that's why uncharted territory due to odds and oh math (can be fun).says I , at almost 40 years old . lol.
This is due to the hydrostatic paradox,it states that the height of the water in any container is independent of the shape of the container. This does make sense since it is only the height of the fluid relative to ground which determines the pressure. P r e s s u r e = h × ρ × g where, h = h e i g h t , ρ = d e n s i t y , a=accelaration due to gravity Therefore the shape of the container does not make any difference.