Any larger pairs after this?
1 + 2 + ⋯ + 1 0 1 + 2 + ⋯ + 1 3 = 1 2 + 2 2 + ⋯ + 5 2 = 1 2 + 2 2 + ⋯ + 6 2 ⋮
Find the next pair of integers ( M , N ) larger than ( 1 3 , 6 ) such that 1 + 2 + ⋯ + M = 1 2 + 2 2 + ⋯ + N 2 . Submit your answer as M + N .
The answer is 730.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
C++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
|
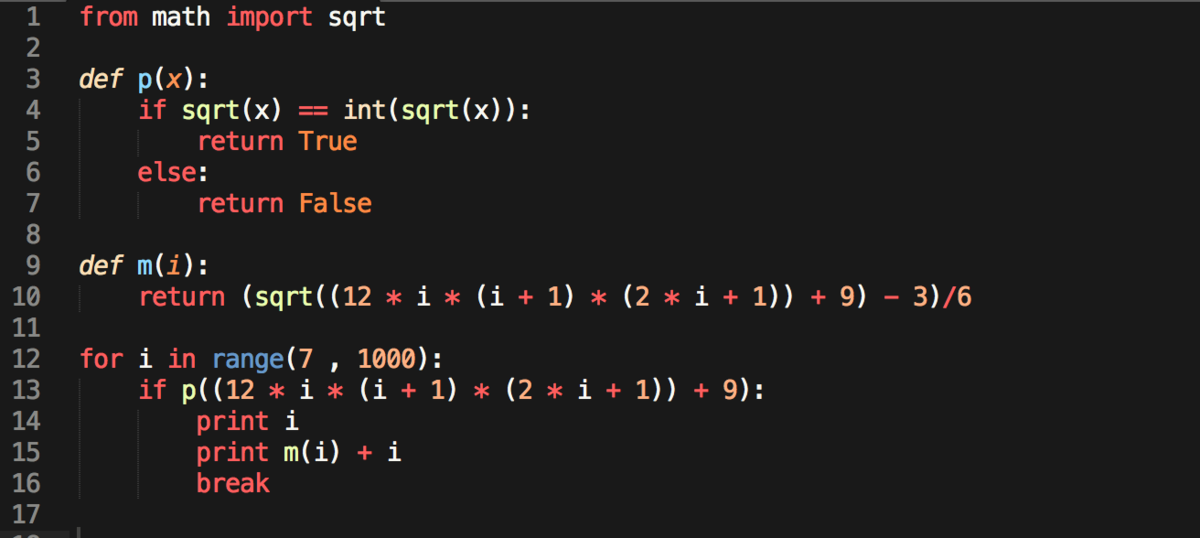
I don't know how to use Python in Brilliant Solution -
Here is the python code -
M = 0
N = 0
for i in range (1000):
M += i
N = 0
for j in range (M+1):
N += (j*j)
if N == M:
print (N + M)
Output = 7 3 0
We get the next pair as - ( 6 4 5 , 8 5 )
I found it easier to use m as the driver. The sum of consecutive integers is 2 1 n ( n + 1 ) and the sum of squares of consecutive integers is 1 / 6 m ( 1 + m ) ( 1 + 2 m ) . Solving for n in terms of m gives 2 1 ( 3 8 m 3 + 1 2 m 2 + 4 m + 3 − 1 ) . I then created a table of when that expression returned an integer: {{1,1},{10,5},{13,6},{645,85}}.
The most of credit for this solution goes to @Avishek Yadav as he aided me to get the idea of discriminant D must be equal to 3 Y 2 1 + 2 + ⋯ + M = 1 2 + 2 2 + ⋯ + N 2 2 M ( M + 1 ) = 6 N ( N + 1 ) ( 2 N + 1 ) 3 M 2 + 3 M − N ( N + 1 ) ( 2 N + 1 ) = 0 M = 6 − 3 ± 3 ( 8 N 3 + 1 2 N 2 + 4 N + 3 ) Now noting the discriminant of above equation D = 8 N 3 + 1 2 N 2 + 4 N + 3 = 8 ( N + 2 1 ) 3 − 2 ( N + 2 1 ) + 3 = X 3 − X + 3 c c c c c c let x = 2 ( N + 2 1 ) It is vivid that discriminant D in the above equation will be perfect square iff D = 3 Y 2 X 3 − X + 3 = 3 Y 2 ⋯ ( a ) The solution of equations a has been provided by Saburô Uchiyama and one can Google it as Solution of a Diophantine equation by sabur o ˆ Uchiyama
So the solution for M , N can be interred as ( 0 , 0 ) , ( 1 , 1 ) ( 1 0 , 5 ) , ( 1 3 , 6 ) , ( 6 4 5 , 8 5 )