Any way you slice it
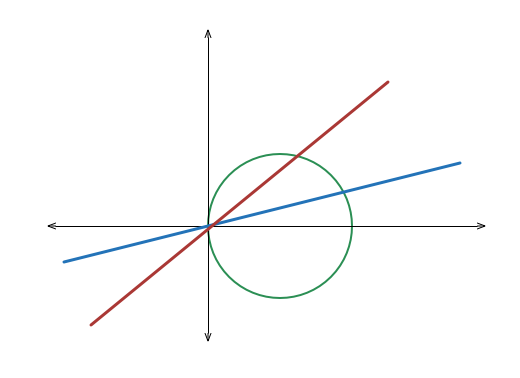 Suppose that two distinct lines passing through the origin cut through the region
R
in the first quadrant bounded by the
x
-axis and the circle
(
x
−
1
)
2
+
y
2
=
1
such that the lines divide
R
into
3
subregions of equal area.
Suppose that two distinct lines passing through the origin cut through the region
R
in the first quadrant bounded by the
x
-axis and the circle
(
x
−
1
)
2
+
y
2
=
1
such that the lines divide
R
into
3
subregions of equal area.
If the sum of the slopes of these two lines is S , find ⌈ 1 0 0 0 ∗ S ⌉ .
Note: Numerical methods can be used in the process of solving this question.
The answer is 939.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
It's so frustrating when you realize at the end of the problem that you have worked with 2 decimals all this time and you get something like 945 while the answer is 939. This problem is about visualizing and using Sector + Segment area for the geometric approach. It is a nice problem anyway
Log in to reply
Wish You a Merry Christmas and a Happy New Year
Since the answer requires 1000S, at least four significant digit is the minimum !!
Very Nice problem and Nice solution as always Sir Brian Charlesworth. At first I used calculus but it turned out to be very tedious so I tried a geomtric approach That gave me a very Small equation to work with.
Log in to reply
Thanks, Oussama. When I first thought of the question I initially tried calculus as well, only to realize, as you did, that it was not the best approach.
Wish You a Merry Christmas and a Happy New Year
For the second slope I have taken upper two regions and , like the first the equation of the sector with area now 3 π ? I remember a few months back you had explained how to find the area of a circular sector. I had used graphing calculator ti-83 Plus to graph the equation with zoom box for accuracy. Calculus was the first thought, but soon realized the geometry is very simple.
Log in to reply
Yes, that's an even more efficient approach, since you are using the same "method" to find each of the slopes. Thanks for mentioning this. :)
I thought all problems on here could be solved without numerical methods, so I toiled away on the geometric and calculus-based problems and found that both equations needed to be solved with numerical methods! Incredibly annoying.
Log in to reply
I'm sorry for the frustration this caused you. Numerical methods are an essential tool in mathematics so I thought that their use would be acceptable. I've solved and posted other problems where they were a part of the solution process, so I don't think that there is any rule that they are forbidden on this site. That being said, to avoid having others experience the same frustration, I will add a note saying that numerical methods are allowed in the process of solving this problem.
Log in to reply
That would be appreciated; I wouldn't mind finding myself using numerical methods if I knew they were acceptable. In general I force myself to use only scientific calculator functions.
Nice solution, I don't quite understand it but it seems similar to how I solved this problem. I found the area of the circle center then subtracted th area of the triangle with verticies at the end points of the red line and at the circle's center.
Log in to reply
Wish You a Merry Christmas and a Happy New Year
For the lower subregion, why the angle is 2 π − α ? Isn't it just π − α ? The first one is the angle at (0,0), and we can't calculate the triangle area just by this angle. Isn't the triangle area 2 r 2 sin ( π − α ) cos ( π − α ) ? In my calculations, this angle is 0.264093796 rad...
Log in to reply
Rereading my solution I realize I was short on the details of this calculation. The angle α is the central angle between the radial line from the center of the circle to the point of intersection of the lower (blue) line and the circle. This lower subregion can then be divided into a circular sector with central angle α and an isosceles triangle with equal sides being radial lines of the circle with an angle of π − α between these two equal sides.
The area of the circular sector is 2 1 r 2 α = 2 α .
For the triangle, we can first divide it into two congruent right triangles, each with a hypotenuse length 1 and legs with lengths sin ( 2 π − α ) = cos ( 2 α ) and cos ( 2 π − α ) = sin ( 2 α ) .
Each of these congruent right triangles thus has an area of 2 sin ( 2 α ) cos ( 2 α ) , and so our original triangle has an area of sin ( 2 α ) cos ( 2 α ) = 2 sin ( α ) .
Since the combined areas of the sector and triangle equal that of the lower subregion, we find that
2 α + 2 sin ( α ) = 6 π ⟹ α + sin ( α ) = 3 π ,
in agreement with the equation in my posted solution. We could also have noted right away that with the central angle being α , by symmetry the angle between the lower (blue) line and the positive x -axis must be 2 α , at which point we could have proceeded with the area calculations as before.
Log in to reply
Yes... yes... Now I see your steps and I've realized the mistake in my calculations... Thanks!
numerical methods ??
Log in to reply
One could use Newton's Method, but to save time I just used WolframAlpha. :)
I would just point out that the equation α + sin ( α ) = 3 π can also be used for the other line, if you use 3 2 π instead of 3 π . (Not that there's a problem with your solution, I'm just mentioning a variation.)
sin − 1 1 + m 2 1 − 4 1 sin ( 4 sin − 1 1 + m 2 1 ) - ( 1 + m 2 ) 2 2 m = g ( m ) = 6 π o r 3 π gives direct iterated m 2 and m 1 .
Converting the curve into polar form, we have:
( x − 1 ) 2 + y 2 = 1 x 2 + y 2 − 2 x = 0 r 2 − 2 r cos θ = 0 ( r − cos θ ) 2 − cos 2 θ = 0 r = cos 2 θ + cos θ r = 2 cos θ
Let the equation of the red line be y = k 1 x , and the equation of the blue line be y = k 2 x . These lines represent the lines θ = tan − 1 k 1 and θ = tan − 1 k 2 on the polar graph respectively. We now need the following to be true:
2 1 ∫ 0 tan − 1 k 1 ( 2 cos θ ) 2 d θ = 3 π and 2 1 ∫ 0 tan − 1 k 2 ( 2 cos θ ) 2 d θ = 6 π
Firstly,
2 1 ∫ ( 2 cos θ ) 2 d θ = 2 ∫ cos 2 θ d θ = ∫ cos 2 θ + 1 d θ = 2 1 sin 2 θ + θ + C
Therefore
[ 2 1 sin 2 θ + θ ] 0 tan − 1 k 1 = 3 π and [ 2 1 sin 2 θ + θ ] 0 tan − 1 k 2 = 6 π
This gives us k 1 = 0 . 6 6 4 2 2 … and k 2 = 0 . 2 7 4 7 5 …
Therefore S = 0 . 9 3 8 9 7 … and ⌈ 1 0 0 0 S ⌉ = ⌈ 1 0 0 0 ( 0 . 9 3 8 9 7 … ) ⌉ = ⌈ 9 3 8 . 9 7 … ⌉ = 9 3 9 .
Nice solution! Thanks for posting it. :)

The strategy is to solve in rotated co-ordinates.This makes the problem simpler and easy to visualize.
My solution is identical to the Brian.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
|
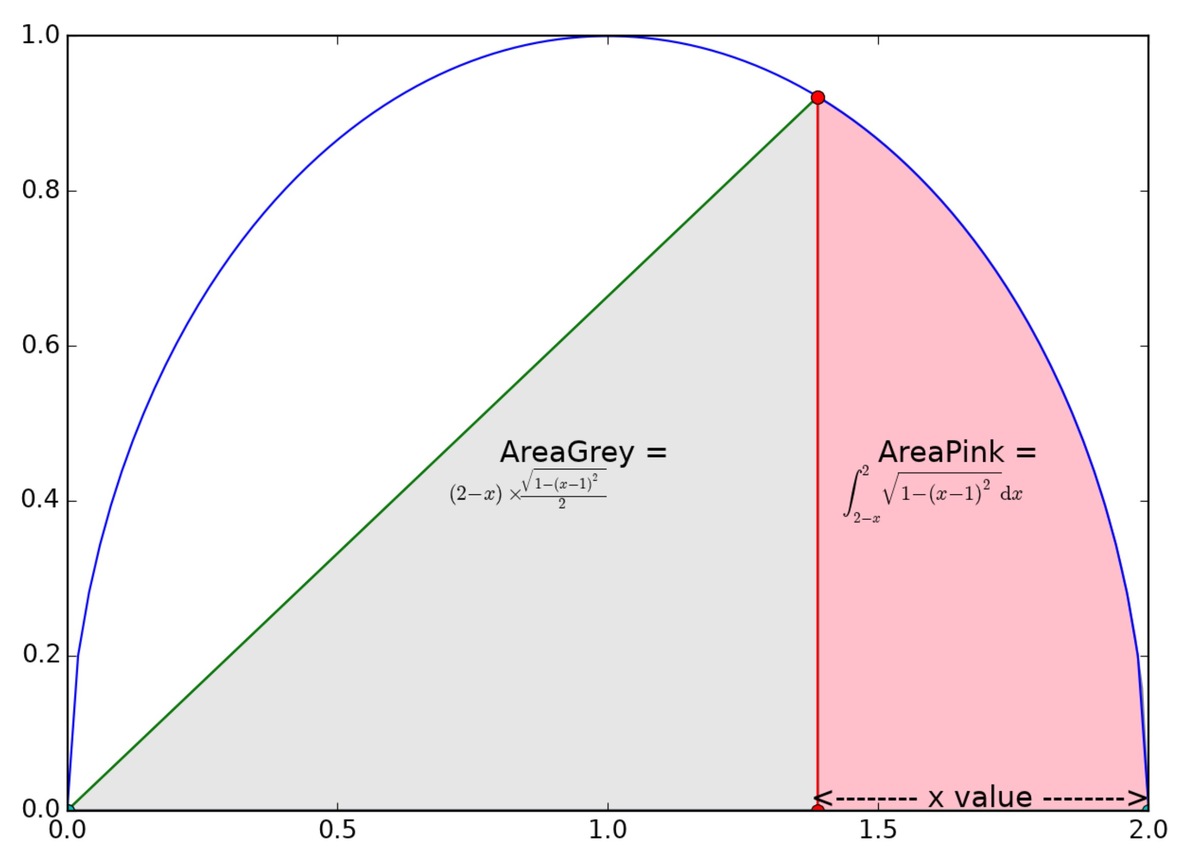
Since there has been the best way provided by others, I would only tell you another way but not in detail about its every single step. However, you can see the consequence and get some idea about what happens.
Most immediate way may not be an ultimate choice, but it can be fastest in a situation. I applied integration. Since iteration method is expected, type of approach applied is not critical.
y = 1 − ( x − 1 ) 2
⇒ y = x ( 2 − x )
To intercept with y = m x ,
( m x ) 2 = ( x ( 2 − x ) ) 2 .
x = 1 + m 2 2 and y = 1 + m 2 2 m
Therefore, ( 1 + m 1 2 2 , 1 + m 1 2 2 m 1 ) and ( 1 + m 2 2 2 , 1 + m 2 2 2 m 2 ) are the points of lines intercept with the semicircle.
My convention here is following the sequence of angle about positive x-axis for anti-clockwise of 1, 2 and 3!
Let A 1 = ( 1 + m 1 2 ) 2 2 m 1 + ∫ 1 + m 1 2 2 2 x ( 2 − x ) d x
A 3 = ∫ 0 1 + m 2 2 2 x ( 2 − x ) d x - ( 1 + m 2 2 ) 2 2 m 2
A 2 = ( 1 + m 2 2 ) 2 2 m 2 + ∫ 1 + m 2 2 2 1 + m 1 2 2 x ( 2 − x ) d x - ( 1 + m 1 2 ) 2 2 m 1 {For purpose to check.}
A 1 = A 2 = A 3 = 6 π since π 1 2 ÷ 6 = 6 π for radius of 1.
Let x = 2 sin 2 θ , d x = 4 sin θ cos θ d θ and θ = sin − 1 2 x :
∫ x ( 2 − x ) d x = θ − 4 1 sin 4 θ + C
A 1 = 6 π = ( 1 + m 1 2 ) 2 2 m 1 + 2 π − sin − 1 1 + m 1 2 1 + 4 1 sin ( 4 sin − 1 1 + m 1 2 1 )
⇒ sin − 1 1 + m 1 2 1 − 4 1 sin ( 4 sin − 1 1 + m 1 2 1 ) - ( 1 + m 1 2 ) 2 2 m 1 = 2 π − 6 π = g ( m 1 ) = 3 π
A 3 = sin − 1 1 + m 2 2 1 − 4 1 sin ( 4 sin − 1 1 + m 2 2 1 ) - ( 1 + m 2 2 ) 2 2 m 2 = g ( m 2 ) = 6 π
Here we are, g ( m 1 ) = 3 π while g ( m 2 ) = 6 π for same function!
By iteration where only one value for each, m 1 and m 2 are obtainable d i r e c t l y with Excel:
1 2 3 4 |
|
m 1 = 0.27474969504639+
m 2 = 0.66422738787590+
A 2 = ( 1 + m 2 2 ) 2 2 m 2 + sin − 1 1 + m 1 2 1 − 4 1 sin ( 4 sin − 1 1 + m 1 2 1 ) − sin − 1 1 + m 2 2 1 + 4 1 sin ( 4 sin − 1 1 + m 2 2 1 ) − ( 1 + m 1 2 ) 2 2 m 1 = 6 π for checking purpose. Verified to match for being exact value of 6 π = 0.523598775598299 as proximity to confirm correct.
As I like to find iterated values to high accuracy, my figures are very accurate.
⌈ 1 0 0 0 × 0 . 9 3 8 9 7 7 0 8 2 9 2 2 2 9 2 ⌉ = 9 3 9
Answer: 9 3 9
The 3 subregions will each have an area of 6 π .
For the "upper" subregion, let 2 θ be the angle subtended by the chord formed by the intersection of the circle with the line of greater slope. Then the area of this subregion is the area of the sector defined by the angle 2 θ minus the area of the triangle with the endpoints of the chord and the point ( 1 , 0 ) as vertices. This gives us the equation
θ − sin ( θ ) cos ( θ ) = 6 π ,
which, by way of numerical methods, has solution θ = 0 . 9 8 4 4 8 4 . . . radians. The angle that the line makes with the x -axis is then 2 π − θ , and so the slope of the line is tan ( 2 π − θ ) = 0 . 6 6 4 2 2 7 9 . . . .
For the "lower" subregion, let α be the angle between the x -axis and the radial line to the (non-origin) endpoint of the chord formed by the intersection of the circle with the line of least slope. Then the area of this subregion will be the sum of the areas of the sector defined by α and the triangle with the endpoints of the chord and the point ( 1 , 0 ) as vertices. This gives us the equation
2 α + sin ( 2 π − α ) cos ( 2 π − α ) = 6 π ⟹ α + sin ( α ) = 3 π ,
which, by way of numerical methods, has solution α = 0 . 5 3 6 2 6 7 . . . . The angle that the line makes with the x -axis is then 2 π − 2 π − α = 2 α , and so the slope of the line is tan ( 2 α ) = 0 . 2 7 4 7 4 9 7 . . . . .
The sum of the two slopes is then
S = 0 . 6 6 4 2 2 7 9 . . . + 0 . 2 7 4 7 4 9 7 . . . . = 0 . 9 3 8 9 7 7 6 . . . ,
and so ⌈ 1 0 0 0 ∗ S ⌉ = 9 3 9 .
Here is a diagram of the solution lines. (Ignore the lower part of the circle.)