AP and GP
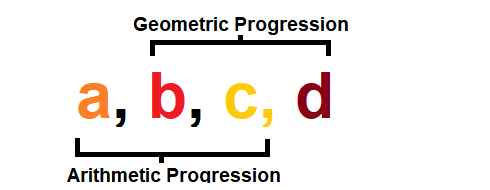
We have four numbers written in a row. The first three numbers are in AP (arithmetic progression) of common difference equal to 6 and the last three numbers are in GP (geometric progression) of unknown common ratio. The first number is equal to the fourth number.
What is the sum of all of these numbers?
The answer is -14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We are given that a , b and c are in an arithmetic progression with common difference 6
a = x b = x + 6 c = x + 1 2
b , c and d are in a geometric progression, and its common ratio is
r = b c = x + 6 x + 1 2
Which implies that
d = r c = x + 6 ( x + 1 2 ) 2
But we are also given that a = d , so
a = d ⟺ x = x + 6 ( x + 1 2 ) 2 ⟺ x ( x + 6 ) = ( x + 1 2 ) 2 ⟺ x 2 + 6 x = x 2 + 2 4 x + 1 4 4 ⟺ 1 8 x = − 1 4 4 ⟺ x = − 8
To conclude
( a , b , c , d ) = ( − 8 , − 2 , 4 , − 8 )
And thus
a + b + c + d = − 8 − 2 + 4 − 8 = − 1 4