Apollonian Gasket With Some Numbers
A number of tangent circles are inscribed inside a blue circle as follows:
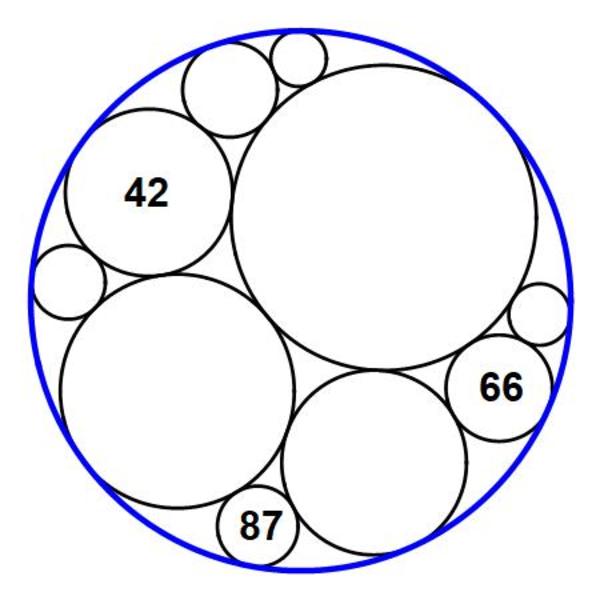
The numbers 4 2 , 6 6 , 8 7 inside some of them are inverses of their radii, so that their radii are actually 4 2 1 , 6 6 1 , 8 7 1 .
What's the inverse of the radius of the blue circle?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I'll be damned. I was struggling to do this for over 5 hours.
First, I picked out an integral Apollonian gasket starting with − 1 3 , 2 3 , 3 0 , 3 8 , generated some more tangent circles, and then picked 3 of them that would allow a complete solution using just four equations. Exactly how you've done it here. Well done.
If any four mutually tangent circles have integer curvatures, then all the rest have integer curvatures. This is because if
k 4 = k 1 + k 2 + k 3 − 2 k 1 k 2 + k 2 k 3 + k 3 k 1
is an integer, then
k 5 = k 1 + k 2 + k 3 + 2 k 1 k 2 + k 2 k 3 + k 3 k 1
is also an integer.
Is the answer unique?
I can't find another solution, but if we were to assume that all the radii of these circles are unit fractions, then I can prove that the leftmost inscribed circle must have a radius, 1 / r must satisfying r < 2 3 ( 6 1 + 1 6 4 9 ) . What's left is to prove by inspection that this is the only solution.
Here's my failed attempt if we don't make such an assumption:
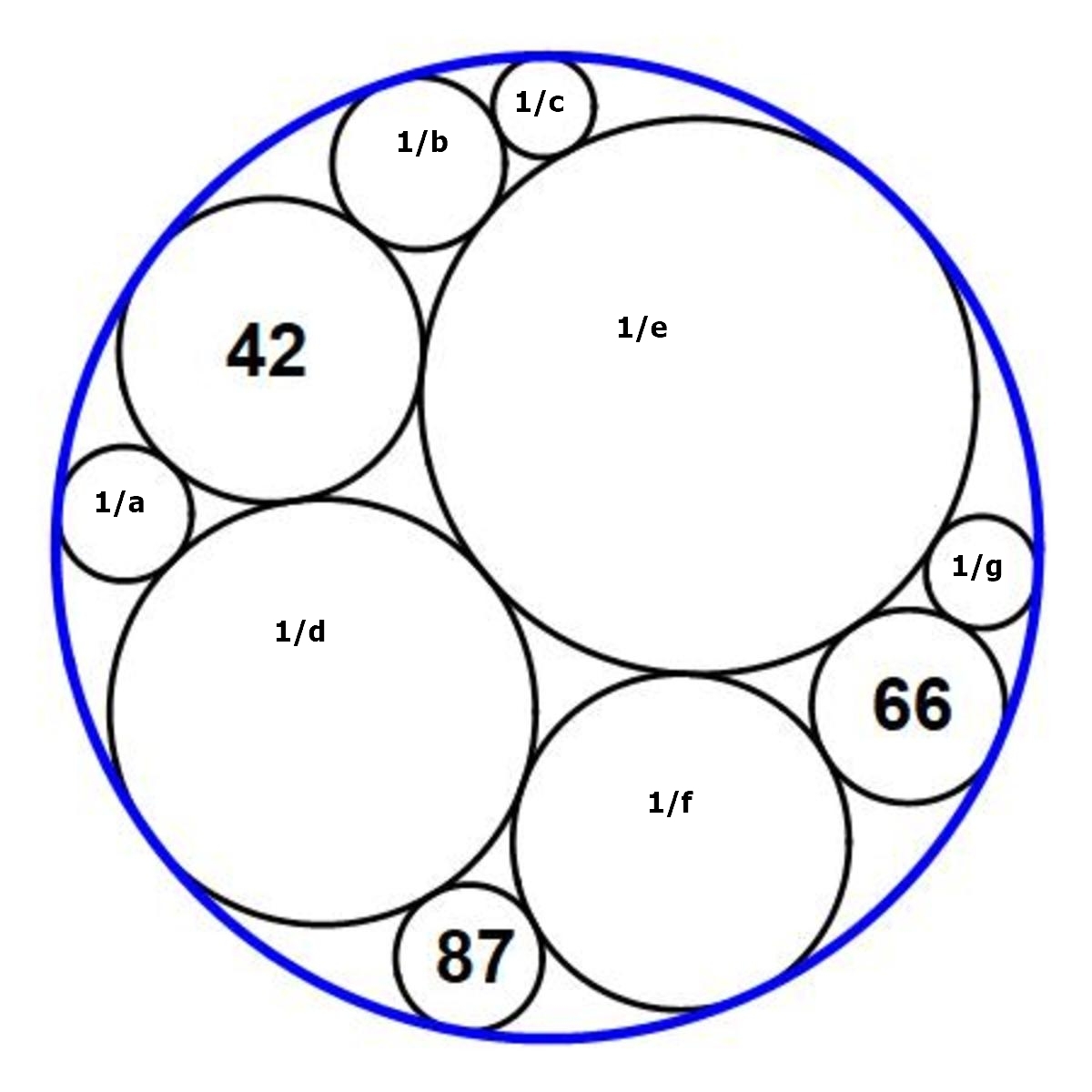
Label the radii as shown above.
Using Descartes Kissing Circle theorem, we can form equations like
( e + f + 6 6 − R ) 2 = 2 ( e 2 + f 2 + 6 6 2 + R 2 ) ( e + b + 4 2 − R ) 2 = 2 ( e 2 + b 2 + 4 2 2 + R 2 ) ⋮
If we subtract the two equations whose triplet of radii are ( e , b , 4 2 ) and ( e , d , 4 2 ) , we get 2 R = 2 e − b + d + 8 4
If we subtract the two equations whose triplet of radii are ( e , f , 6 6 ) and ( e , d , f ) , we get 2 R = 2 e − f − g + 1 3 2
If we subtract the two equations whose triplet of radii are ( e , d , f ) and ( 8 7 , d , f ) , we get 2 R = 2 d + 2 f − e − 8 7
If we subtract the two equations whose triplet of radii are ( e , b , 4 2 ) and ( e , b , c ) , we get 2 R = 2 e + 2 b − 4 2 − c
If we subtract the two equations whose triplet of radii are ( e , d , 4 2 ) and ( a , d , 4 2 ) , we get 2 R = 2 d + 8 4 − e − a
Equating these 5 equations together shows that ( d , e , f , g ) = ( − 3 b + c + 1 2 6 , 3 − a − 8 b + 3 c + 3 7 8 , 2 1 7 1 − a , 2 a − 4 b + 2 c + 1 7 7 ) .
Notice that if the Descartes kissing circle equation formed with radii ( 4 2 , d , a ) or with radii ( 4 2 , d , e ) is the same, thus a and e must be the root (in x ) of the equation
( 4 2 + d + x − R ) 2 = 2 ( 4 2 2 + d 2 + x 2 + R 2 )
Solving for x gives two values a and e . By summing these two roots, we can then set R as the subject, R = 6 1 ( − 2 a + 1 0 b + 3 c + 6 3 0 ) .
That's where I'm stuck.
It's unique, Pi Han Goh.
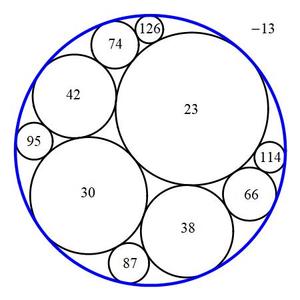
We can ignore the smaller circles. Let A , B , C be the curvatures of the largest three circles, going counterclockwise from the top (so that A ≤ B ≤ C ). Let K be the curvature of the external circle; this will be negative since it is externally tangent to the rest of the circles.
By Descartes' circle theorem we get the four equations ( A + B + C + K ) 2 ( A + B + 4 2 + K ) 2 ( A + 6 6 + C + K ) 2 ( 8 7 + B + C + K ) 2 = 2 ( A 2 + B 2 + C 2 + K 2 ) = 2 ( A 2 + B 2 + 4 2 2 + K 2 ) = 2 ( A 2 + 6 6 2 + C 2 + K 2 ) = 2 ( 8 7 2 + B 2 + C 2 + K 2 ) Subtracting the second equation from the first and simplifying gives ( C − 4 2 ) ( C + 4 2 + 2 A + 2 B + 2 K ) 2 A + 2 B + 2 K 2 A + 2 B + 2 C + 2 K = 2 ( C 2 − 4 2 2 ) = C + 4 2 = 3 C + 4 2 Similarly subtracting the third and fourth equations from the first yields 2 A + 2 B + 2 C + 2 K = 3 C + 4 2 = 3 B + 6 6 = 3 A + 8 7 . So B = A + 7 , C = A + 1 5 , K = 2 4 3 − 3 A . Plugging these into the top equation and solving for the resulting quadratic gives − 4 3 3 A 2 + 2 3 4 3 A + 4 1 6 7 9 = 0 which has roots A = 2 3 , − 3 3 7 3 . Since A , B , C must be positive, we must have A = 2 3 , B = 3 0 , C = 3 8 , K = − 1 3 , and the reciprocal of the radius of the external circle is − K = 1 3 .