Apple Roulette

Logic Level 3

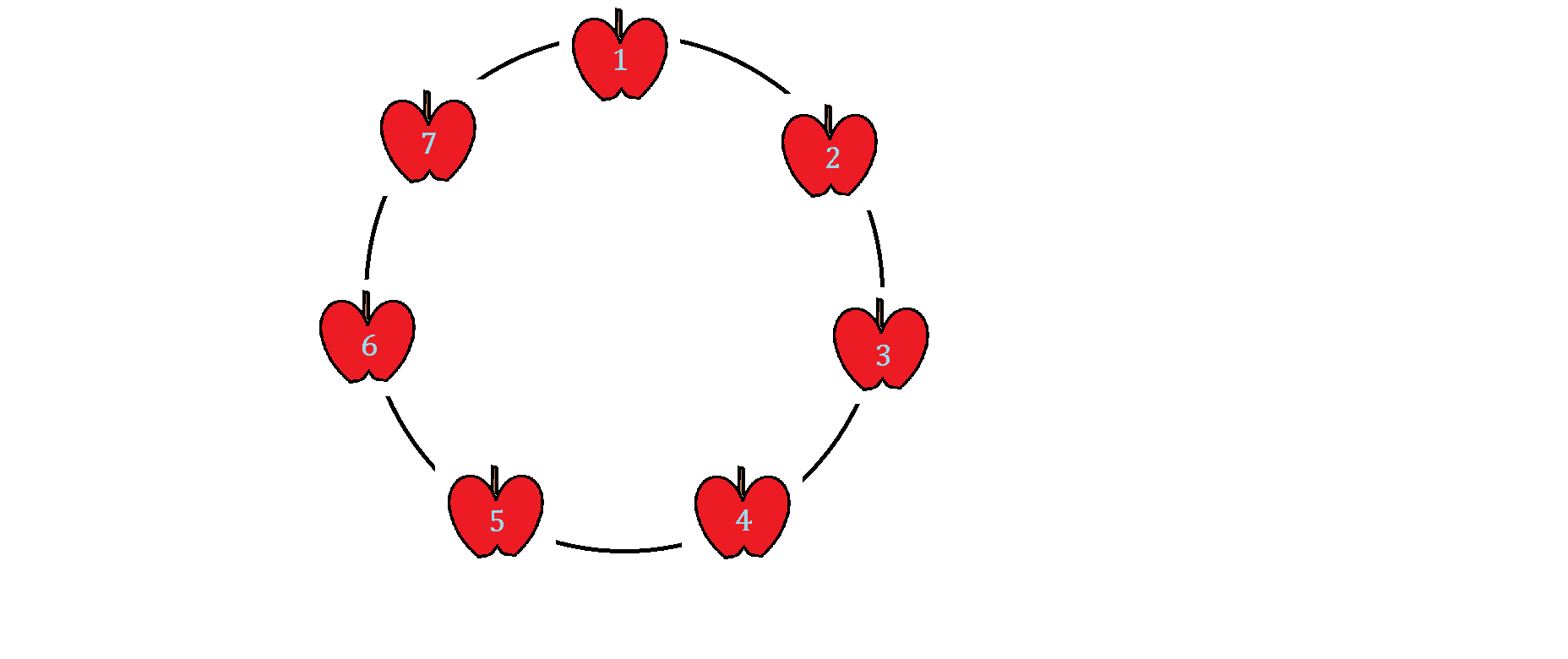
In order to save her throne, the evil queen challenged Snow White to play "Apple Roulette" game: each player would take turns in picking an apple for her opponent to eat from a group of $7$ apples with numbers designated as shown above, where one of them was already dipped with deadly poison. If one survived the test, she would choose the next apple for her opponent.

Snow White accepted the challenge, and so the evil queen randomly picked the first apple for the Princess, who could ate it with no harmful effects. Then Snow White chose the second apple next to the one she ate in the clockwise fashion (For example, if she had eaten #1, she would choose #3 for her stepmother.). Afterwards, the evil queen could also survive her first apple and chose the third apple next to the one she ate in the clockwise fashion.

As the game went on, both monarchs resumed the same choosing methods, and when there were only $2$ apples left, the evil queen dared Snow White to eat their last apples at the same time. Brave and beautiful Snow White again accepted the challenge, and soon after taking a bite, the evil queen suffered a painful and quick death due to her own poison. Snow White then ruled peacefully ever after.

If the poisoned apple was #7, which number was the apple Snow White first ate?

2 4 3 1 5 6

1 solution

Francis Kong
Mar 25, 2018

Without loss of generality, if we solve which apples are left at the end by starting at apple number 1, we can simply shift the starting apple by lining up the last apple for the queen with the poisoned apple.

So If we start at snow white eating apple #1:

Queen eats apple #3
Snow white eats apple #6
Queen eats apple #2
Snow white eats apple #7 Last two apples would be #4 and #5 with Queen eating #5 (2nd remaining apple clockwise from #7)

Because the last apple the Queen ate is #7, you would shift 2 apples clockwise and as such the starting apple is $\boxed{3}$ .

To verify:

Snow white eats apple #3
Queen eats apple #5
Snow white eats apple #1
Queen eats apple #4
Snow white eats apple #2

Last two apples would be #6 and #7 with Queen eating #7 (2nd remaining apple clockwise from #2)

Apple Roulette

1 solution

0 pending reports