Applicability of "Long Solenoid" Equation

Electricity and Magnetism Level 5

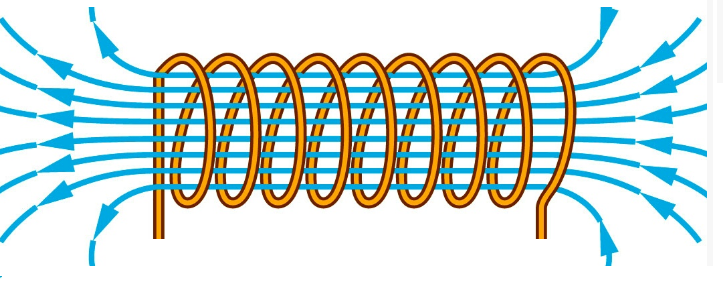
A solenoid consists of many circular turns of wire, as shown in the image (credit to the linked Brilliant wiki). If the length of the solenoid (along its axis) is large compared to the loop radius, we can approximate the magnetic flux density magnitude at the solenoid center using the following equation.

$B = \mu_0 \, n \, I$

In the above equation, $I$ is the current in the solenoid, and $n$ is the number of turns per unit of axial length. If the solenoid isn't very long relative to the loop radius, this approximation breaks down. Let's consider a solenoid with the following geometry:

$x = cos \theta \\ y = sin \theta \\ z = \frac{1}{10} \theta \\ {-2 \pi} \, \frac{N}{2} \leq \theta \leq 2 \pi \, \frac{N}{2}$

The parameter $N$ is the number of turns making up the solenoid, and is constrained to be a multiple of two, for the sake of symmetry. What is the minimum value of $N$ , such that the actual magnetic flux density magnitude at the origin is at least $90 \%$ of the value predicted by the "long solenoid" equation?

The answer is 8.

1 solution

Fiki Akbar
Jun 5, 2018

The magnetic field at point $(0,0,z)$ due to a ring with radius $a$ located on $x-y$ plane is given by (with the current $I$ oriented counter clockwise), $\vec{B}(z) = \frac{\mu_0 I}{2}\;\frac{a^2}{(z^2 + a^2)^{3/2}}\;\hat{z}$

We can make a partition of solenoid with length $2L$ as a thin ring with radius $a$ and thickness $dz$ carries current $dI = n I dz$ . Then, the magnetic field at the center of the solenoid (the origin) is given by $\begin{aligned} \vec{B} & = & \frac{\mu_0 a^2 n I}{2}\int_{-L}^{L}\;\frac{dz}{((z+L)^2 + a^2)^{3/2}}\;\hat{z}\;dz\\ & = & \mu_0 n I\;\frac{L}{\sqrt{L^2 + a^2}}\; \hat{z}\\ & = & \vec{B}_{\mathrm{long}}\;\frac{L}{\sqrt{L^2 + a^2}} \end{aligned}$

Since $B/B_{\mathrm{long}}$ is at least $9/10$ , and it is known $a = 1$ and $L = \frac{\pi N}{10}$ , then at least $N_{\min} = \frac{90}{\pi\sqrt{19}} = 6.7$ However, since $N$ must be multiple of 2, then $N_{\min}=8$ .

Applicability of "Long Solenoid" Equation

The answer is 8.

1 solution

0 pending reports