Application of the Uniform limit theorem

Calculus Level 1

For n ∈ N n\in \mathbb{N} , let f n : [ 0 , π ] → R f_n:[0, \pi]\to \mathbb{R} be defined by

f n ( x ) : = sin ⁡ n ( x ) f_n(x):= \sin^n (x)

Is the sequence { f n } n = 1 ∞ \{f_n\}_{n=1}^{\infty} uniformly convergent?

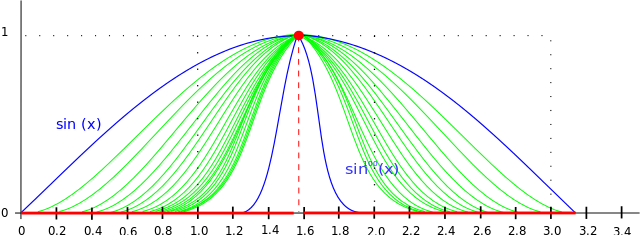
Hint : is the limit function continuous?

This problem is often posed in calculus textbooks.
No Yes

Ognjen Vukadin by Ognjen Vukadin , 38, Austria

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ognjen Vukadin
Jul 15, 2016

The limit function is discontinuous:

f ( x ) = { 1 , x = π 2 0 , x ∈ [ 0 , π ] ∖ { π 2 } f(x) = \begin{cases} 1, & x = \frac{\pi}{2} \\ 0, & x\in [0,\pi]\setminus \{\frac{\pi}{2}\} \\ \end{cases}

Uniform limit theorem implies that this can happen only if convergence is not uniform since all the functions f n f_n are continuous.

7 Helpful 0 Interesting 2 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...