Apply Midpoint Theorem?

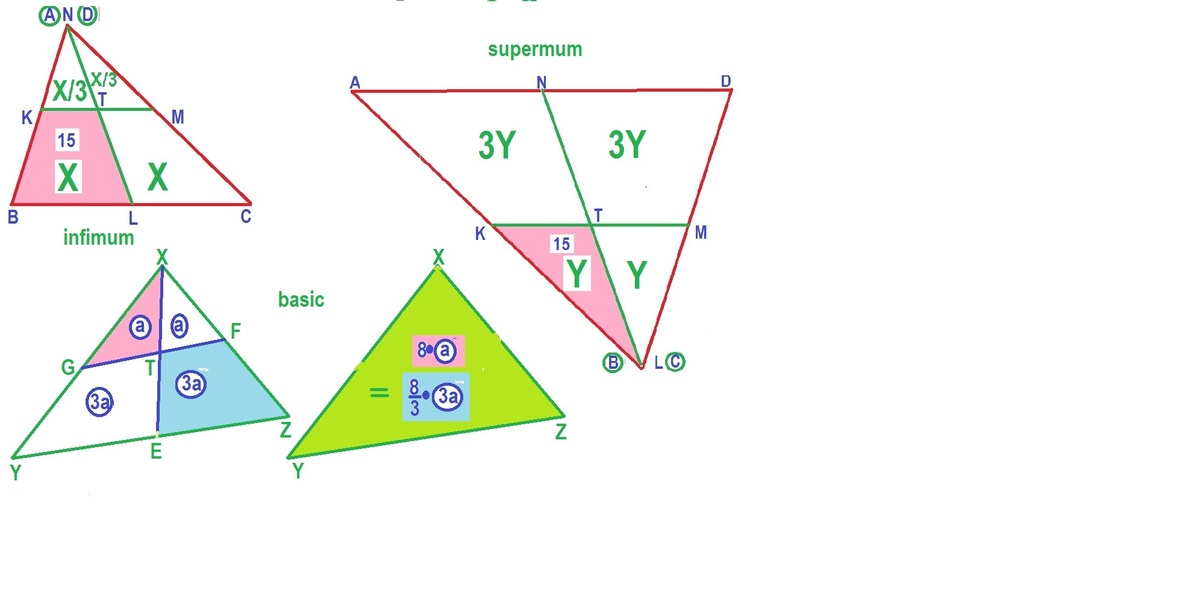
We will create a bound for $|ABCD|$ in terms of $|BKTL|$ .

We will first find a lower bound.

By Midpoint Theorem, $KL \parallel AC \parallel MN$ and $KN \parallel BD \parallel LM$ . Thus, $KLMN$ is a parallelogram and $|KLT|=|LMT|=|MNT|=|NTK|=\frac{1}{4} |KLMN|$ . Also, since $K$ and $N$ are the midpoints of $AB$ and $DA$ , the length of the perpendicular dropped from $A$ to $KN$ is the same as the length of the perpendicular from a point on $KN$ on to $BD$ . The same applies for the other 3 points. Thus, $|AKN|+|BKL|+|CLM|+|DMN|=|KLMN|$ , which implies $|KLT|=\frac {1}{8} |ABCD|$ .

By similarity, we have $|BKL|=\frac{1}{4}|BCA|$ . We also know that $|BCA|<|ABCD|$ since the quadrilateral is convex and we also know that $|BCA|+\epsilon \leq |ABCD|$ for any small $\epsilon>0$ . Thus, $|BKL|<\frac{1}{4}|ABCD|$ .

From this, we get $|KLT|+|BKL|<\frac{1}{8} |ABCD| + \frac{1}{4} |ABCD|$ , which implies $\frac{8}{3} |BKTL| < |ABCD|$ . Note that this is the tightest lowest bound since the strictly less than case becomes less than or equal to for any sufficiently small $\epsilon>0$ . Thus, the infimum area of $ABCD$ is 40.

We will now find an upper bound.

We have that $|BKL|>0$ , and this is obviously the tightest bound since for any small $\epsilon>0$ , we have that we can construct a quadrilateral with that area. We also have that $|KLT|=\frac{1}{8}|ABCD|$ . Thus, $|BKL|+|KLT|>\frac{1}{8} |ABCD|$ , which implies $8|BKTL|>|ABCD|$ , which we have shown to be the supremum. Thus, the supremum area of $ABCD$ is 120.

Thus, the sum of the infimum and supremum areas of $ABCD$ is $120+40=\boxed{160}$ .

In a triangle XYZ, join midpoints F of XY and G of XZ. Join X to E, the midpoint of YZ. FG and XE intersect at T.
The area of each triangle XGT and XFT is equal, and equal to one eighth of triangle XYZ , also equal to one third of each quadrilateral TGYE and TFZE. Area of each quadrilateral is equal and 3/8 of triangle XYZ. This is based on the midpoint Theorem. This results are used below. See the bottom left two sketches.

INFIMUM
Minimum would be when line AND degenerates into a point say N( or line DMC into say M. The result will be the same.) , and quadrilateral ABCD degenerates into triangle NBC. The triangle NBC has midpoints K, M, and L. KM intersect LN at T.
$\therefore\ \dfrac 3 8* Area\ quadrilateral \ KBLT\ =\ full\ area\ \Delta\ NBC.$
So the area of degenerated quadrilateral ABCD=8/3*15=40.

SUPERMUM
Now maximum would be when line BLC degenerates into a point say L ( or line AKB into say K. The result will be the same.) , and quadrilateral ABCD degenerates into triangle BNC. The triangle BNC has midpoints K, M, and L. KM intersect LN at T.
$\therefore\ 8* Area\ \Delta \ BNC\ =\ full\ area\ \Delta\ NBC.$
The area of degenerated quadrilateral ABCD=8*15=120.

So the sum is 40 + 120 = $\color{#D61F06}{160}.$