Applying the Sine and Cosine Rules

Geometry Level pending

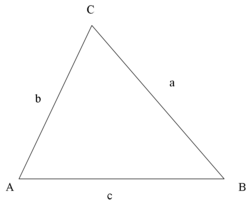As shown above, a triangle is drawn with segments a, b and c with their relative angles A, B and C respectively. When a line, h, is drawn from C to a point on segment c such that the angles between h and c are both 90 degrees, a b h = 1 \frac{ab}{h} = 1 .

If it is also known that t a n A = 3 tanA = 3 and b 2 + c 2 − a 2 = 2 b^2+c^2-a^2 = 2 .

Find a b c abc


The answer is 3.

Steven Lee by Steven Lee , 22, Indonesia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Zi Song Yeoh
Apr 15, 2014

I'm doing this without a diagram.

Firstly, we get a b = h ab = h from the first equation. Now, let S S be the area of the triangle. Then, S = 1 2 c h = 1 2 a b s i n C ⇒ s i n C = c S = \frac{1}{2}ch = \frac{1}{2}absinC \Rightarrow sinC = c . By sine rule, we also have s i n A = a , s i n B = b sinA = a, sinB = b .

Now, cosine law gives a 2 = b 2 + c 2 − 2 b c c o s C a^2 = b^2 + c^2 - 2bccosC . So, 2 b c c o s A = b 2 + c 2 − a 2 2bccosA = b^2 + c^2 - a^2 , which implies b c c o s A = 1 bccosA = 1 or c o s A = 1 b c cosA = \frac{1}{bc} .

Now, 3 = t a n A = s i n A c o s A = a b c 3 = tanA = \frac{sinA}{cosA} = abc . So, a b c = 3 abc = \boxed{3} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

TanA = 3, .... CosA = 1/sqrt(10)... SinA = 3/sqrt(10) = h/b............(1)
App. Cos Rule:- a2 =b2 + c2 - 2 * b * c/sqrt(10)...2 = 2 * b * c/sqrt(10)
b * c/sqrt(10) = 1......ab/h = 1...<....> b * c /sqrt(10) * a * b/h = 1
abc = sqrt(10) * h/b = 3 by (1)


1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...