Approximate the answer based on distances between SSS triangles' upper vertices.
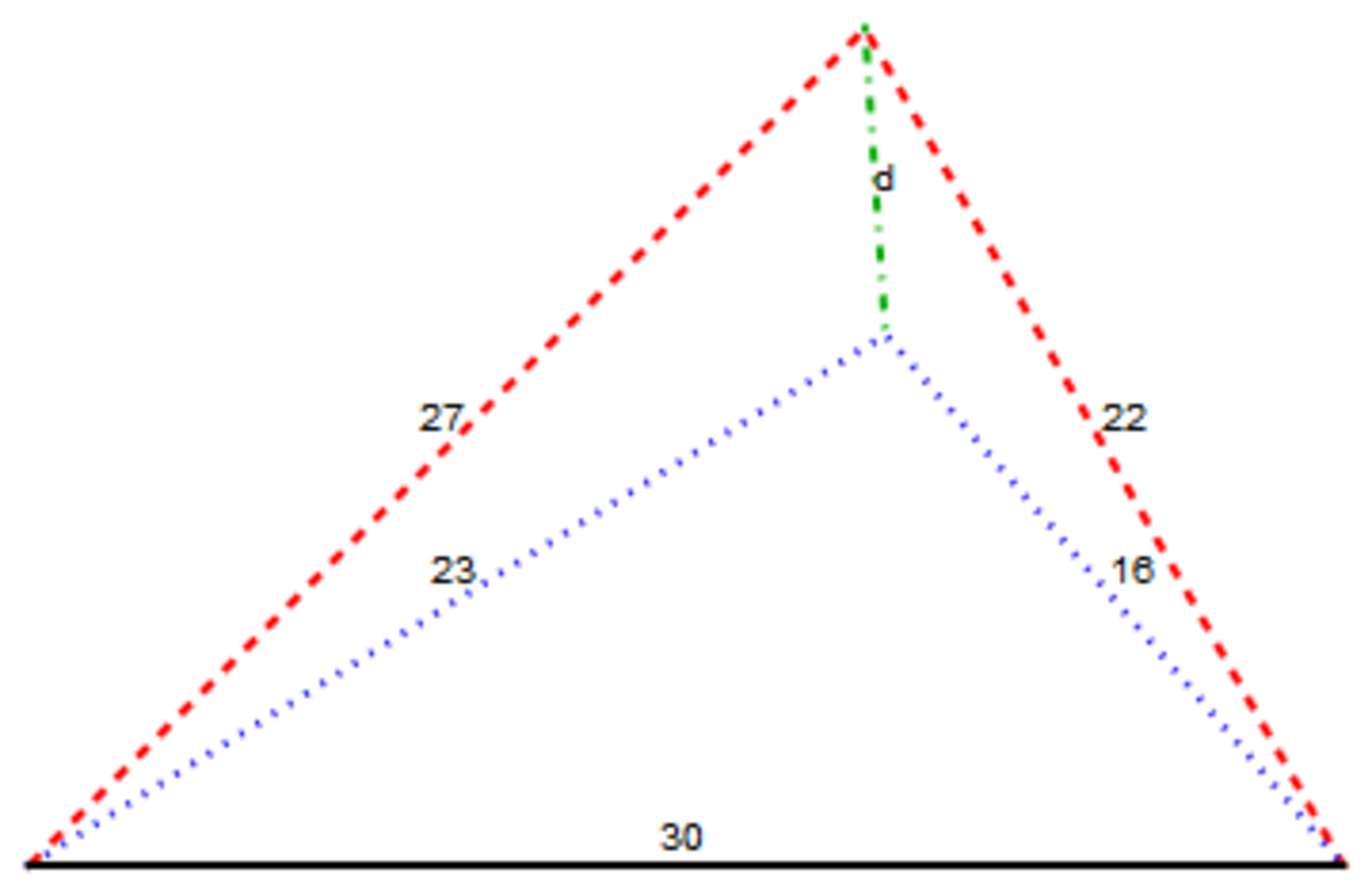
Compute d − ⌈ d ⌋ where ⌈ ⋅ ⌋ means to round to nearest integer. In this case, the value is distinctly close to an integer so that no disambiguation rules are needed.
The answer is 8.57367E-8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The issue is the needed precision of the computations to be able to see the answer. The subtraction of two nearly equal floating point (scientific notation number to some people) causes significant loss of precison. In this case, if the computations were done on a slide rule (at best, four digits of precison) or typical hand calculators (eight digits of precison) are not sufficient to see the difference clearly and with sufficient precison for Brilliant's floating point answer handling (about three percent or between two and three digits of precison). Twelve digits or more are sufficient. Most calculator programs on smart cellphones and Wolfram|Alpha have sufficient precison.
I solved this problem using GeoGebra - check out the link below to see what I did.
Oh, also, to the person who wrote this problem: Maybe include in the description that you need to use scientific notation to solve the problem! I typed 0 in and got it wrong, and I was so sure of myself. But I figured it out anyway haha
That is the intended lesson for this problem. The "distinctly close to an integer" was also a hint.
What was the intended lesson? And the "distinctly close to an integer" part made me think it was something like, for example, 8.92 (or something where the decimal was close to 1 or 0).
Yes. This is not a problem to be solved on a slide rule. In fact, most eight digit hand calculators would have problems with the calculations. As most hand calculators have even number of digits, a hand calculator with 12 digits or more could do the problem, e.g., TI 89, HP 4x series, and the HP Prime.
Okay, that makes sense. I had to use online graphing calculators because I lost my hand-held one. Grr!
:-) I had more problems generating the illustration than doing the problem.
Assuming that the base of both triangles is horizontal and that the left hand ends of the bases are at the origin, the coordinates of the vertices of the larger triangle are { 0 , 0 } , { 3 0 , 0 } , { 1 2 2 2 9 , 1 2 5 2 5 3 5 } and the coordinates of the vertices of the smalle triangle are { 0 , 0 } , { 3 0 , 0 } , { 2 0 3 9 1 , 2 0 2 3 1 1 1 } . The distance d is ( 1 2 5 2 5 3 5 − 2 0 2 3 1 1 1 ) 2 + 2 2 5 4 9 . That value evaluates after rounding to 7 . The difference numerically between 7 and d is about 8.573674836753753E-8 .
I think you will find that the word you want is disambiguation
As it does not change my intent, I changed the spelling in the problem.
Very nice near-integer solution considering how small the side-lengths are. Did you discover this yourself?
Log in to reply
I'm also incredibly curious how he managed to find such "nearly an integer" in an entire setup with no non-integers present. Reminds me of the Fermat's last theorem near misses .
Web searches are very helpful. The search phrase I used is "almost integer". I picked from the more extreme examples to raise the computation precision issue.
Let us label the angles as such. Using cosine rule , we have
cos ( θ 1 ) = 2 ⋅ d ⋅ 2 3 d 2 + 2 3 2 − 2 7 2 , cos ( θ 2 ) = 2 ⋅ d ⋅ 1 6 d 2 + 1 6 2 − 2 2 2 .
With compound angle formula , cos ( A + B ) = cos ( A ) cos ( B ) − sin ( A ) sin ( B ) , we obtain
cos ( 3 6 0 ∘ − ( θ 1 + θ 2 ) ) = cos ( θ 1 + θ 2 ) = cos ( θ 1 ) cos ( θ 2 ) − sin ( θ 1 ) sin ( θ 2 ) = 2 ⋅ 2 3 ⋅ 1 6 2 3 2 + 1 6 2 − 3 0 2 = − 3 2 5 .
Because sin ( A ) = 1 − cos 2 ( A ) for 0 ∘ < A < 1 8 0 ∘ , the equation above can be expanded and simplified to:
9 0 0 d 4 − 9 2 1 3 1 5 d 2 + 4 2 9 8 3 5 3 6 = 0 . Using quadratic formula , and knowing that d > 0 is super duper close to an integer, d = 2 1 3 0 6 1 4 2 1 − 2 2 3 1 5 3 8 8 7 5 9 ≈ 7 + 0 . 0 0 0 0 0 0 0 8 5 7 3 6 7 5 .
Also note that the inradius of the circumcircle of the entire triangle is s s ( s − a ) ( s − b ) ( s − c ) , where a , b , c = 2 7 , 2 2 , 3 0 , s = 2 a + b + c , then r = 3 1 6 1 6 6 2 5 < 8 . So d < 2 r < 1 6 ( d is shorter than the diameter of the circumcircle). Thus, even if we're not told that d is super duper close to an integer, then the other positive root of d (in the quartic equation above) is an extraneous root.
On the other hand, by trial and error, 9 0 0 X 4 − 9 2 1 3 1 5 X 2 + 4 2 9 8 3 5 3 5 = 0 has a root 7, so 9 0 0 X 4 − 9 2 1 3 1 5 X 2 + 4 2 9 8 3 5 3 5 + 1 = 0 has a root larger than 7, but only eensy larger than 7.