Approximating π with hexagons
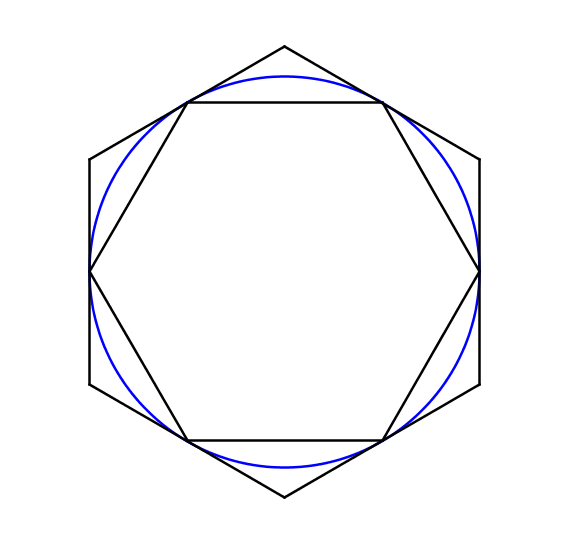
In the figure to the right, a circle is circumscribed around a regular hexagon, and the same circle is inscribed within another regular hexagon.
Let P 1 be the perimeter of the larger hexagon, let P 2 be the perimeter of the smaller hexagon, and let C be the circumference of the circle.
The circumference of the circle can be approximated by finding the mean of the two perimeters:
C ≈ 2 P 1 + P 2 .
If π is approximated using the approximation for circumference above, then π ≈ b a + c , where a , b , c are positive integers, a and b are coprime, and c is square-free.
Find a + b + c .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great question! I love the graphics in your solution.
Nice. What drawing software do you use?
Log in to reply
I use Geogebra to draw the shapes. I'm thinking of trying something else because Geogebra has been really glitchy since I upgraded to Windows 10.
For editing the pictures, I use good old Microsoft Paint :)
For a 6-gon, the relations between circumradius R, inradius r and the side S are, S = 2 R S i n 3 0 = R , r = R C o s 3 0 = 2 3 . C = 2 π ∗ r a d i u s . ∴ If radius = 2 1 , C = π . S m a l l h e x a g o n : − R s = 2 1 . ∴ P 1 = 6 ∗ 2 1 = 3 B i g h e x a g o n : − r B = 2 1 . ⟹ R B = 3 2 ∗ r B = 3 1 ∴ P 2 = 6 ∗ 3 1 = 2 ∗ 3 π ≈ 2 P 1 + P 2 = 2 3 + 2 ∗ 3 = 2 3 + 3 . ∴ a + b + c = 8
Let d be the diameter of the circle.
Let's look at the smaller hexagon first. Drawing the diagonals between opposite vertices of the hexagon yields six equilateral triangles. I've left out the larger hexagon from this picture to keep it from getting cluttered:
Each of these equilateral triangles has side length 2 d , and so the perimeter of the smaller hexagon is 3 d .
Now let's look at the larger hexagon. We'll keep the red dotted segments from before, but we'll also draw segments connecting the opposite vertices of the larger hexagon. The smaller hexagon is removed from the picture:
We can now see that 3 0 − 6 0 − 9 0 triangles are formed with the segments we've drawn.
We can use these special right triangles to determine that the large hexagon has side length 3 3 d . Therefore, the perimeter of the large hexagon is 2 3 d .
Now that we have both perimeters, we can approximate the circumference of the circle:
C ≈ 2 P 1 + P 2 = ( 2 2 3 + 3 ) d = ( 2 3 + 3 ) d
π = d C , and so π ≈ 2 3 + 3 .
a = 3 , b = 2 , and c = 3 . Thus, a + b + c = 8 .