Arbitrary Points
A horizontal line parallel to the base of a square consists of two arbitrary points. Triangles are drawn as shown in the figure. What fraction of the square is shaded? Give your answer as a decimal.
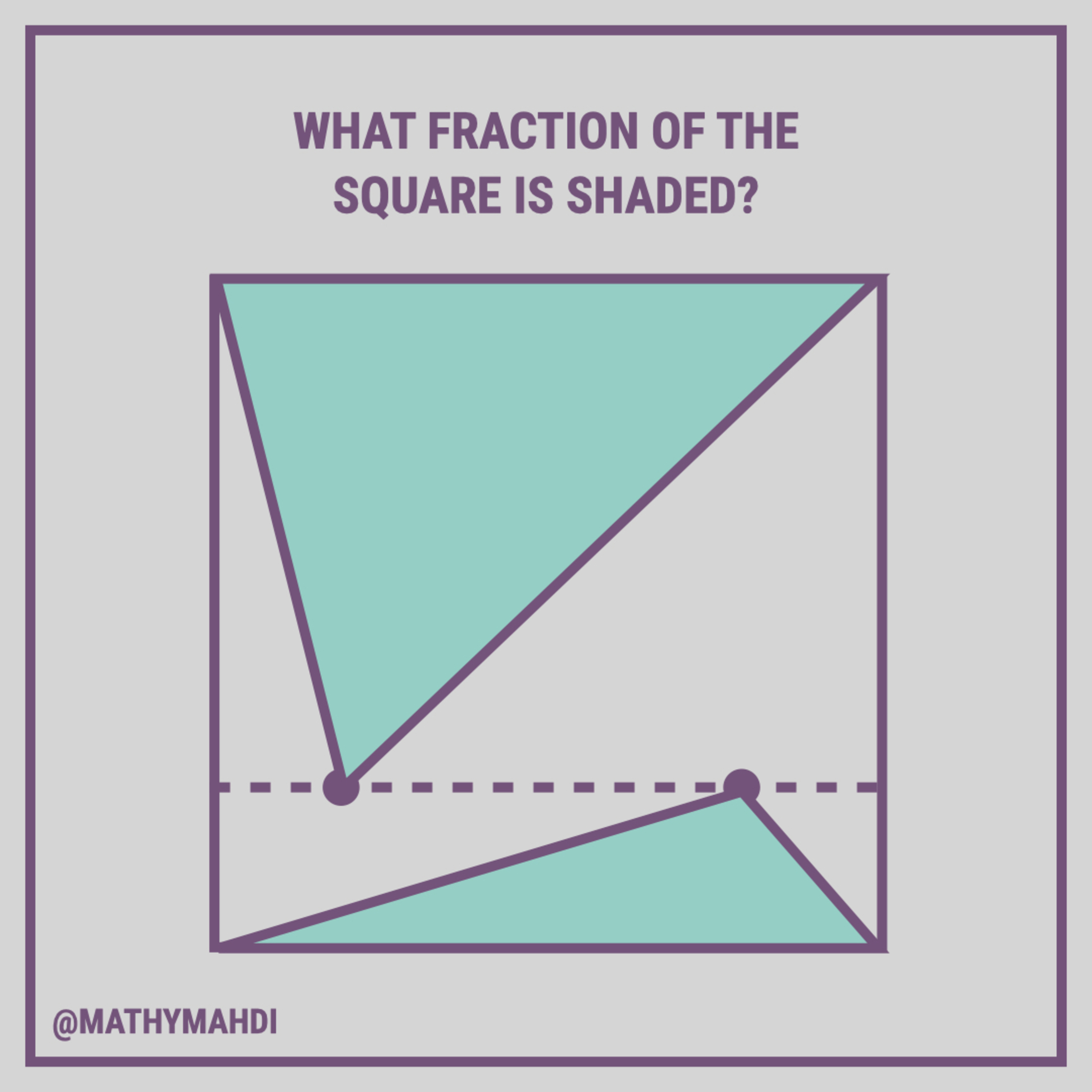
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
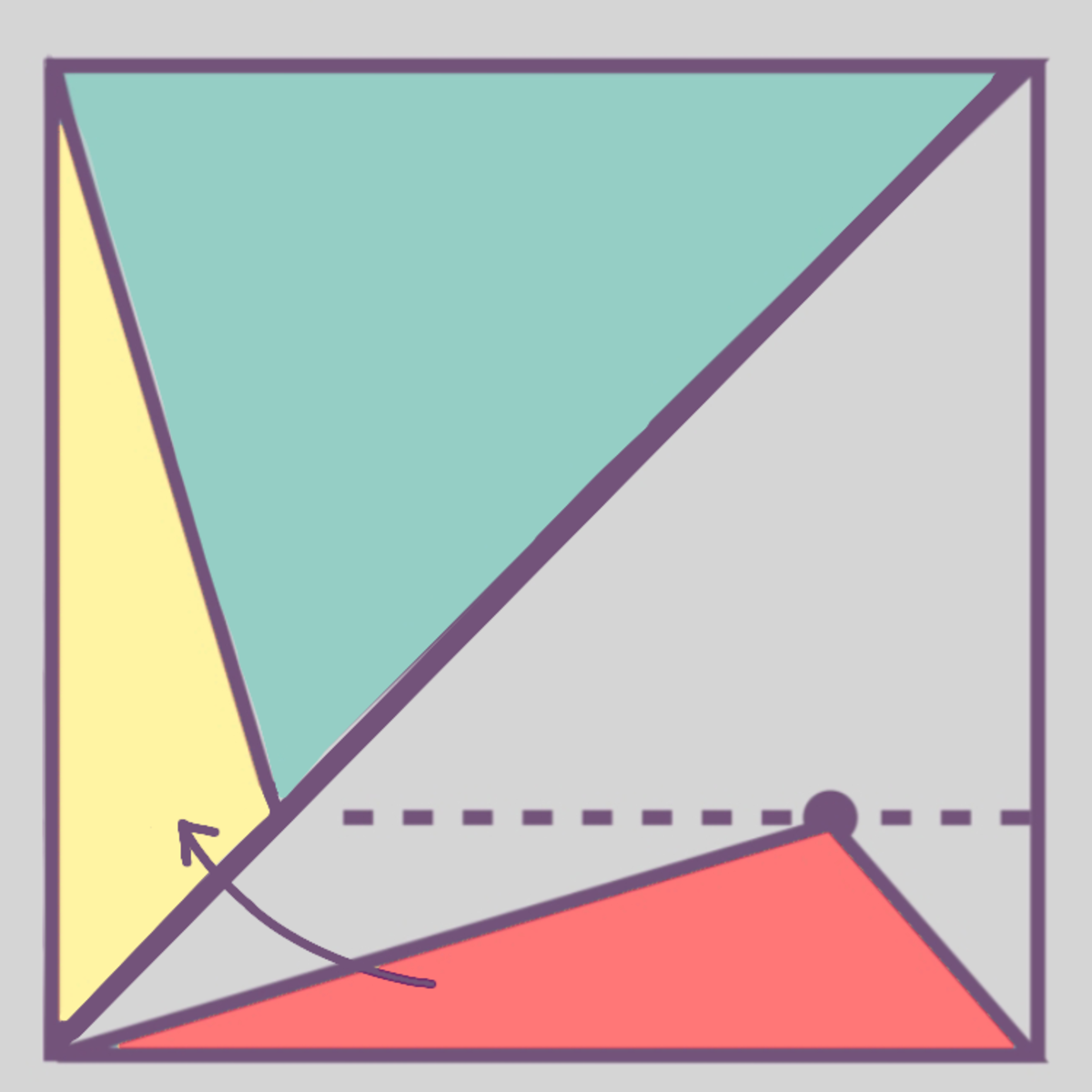
If you partition the diagram as follows:
then A ≅ A ′ , B ≅ B ′ , C ≅ C ′ , and D ≅ D ′ , so that the shaded part equals the unshaded part, and 5 0 % = 0 . 5 of the square is shaded.