Archimedean Siblings
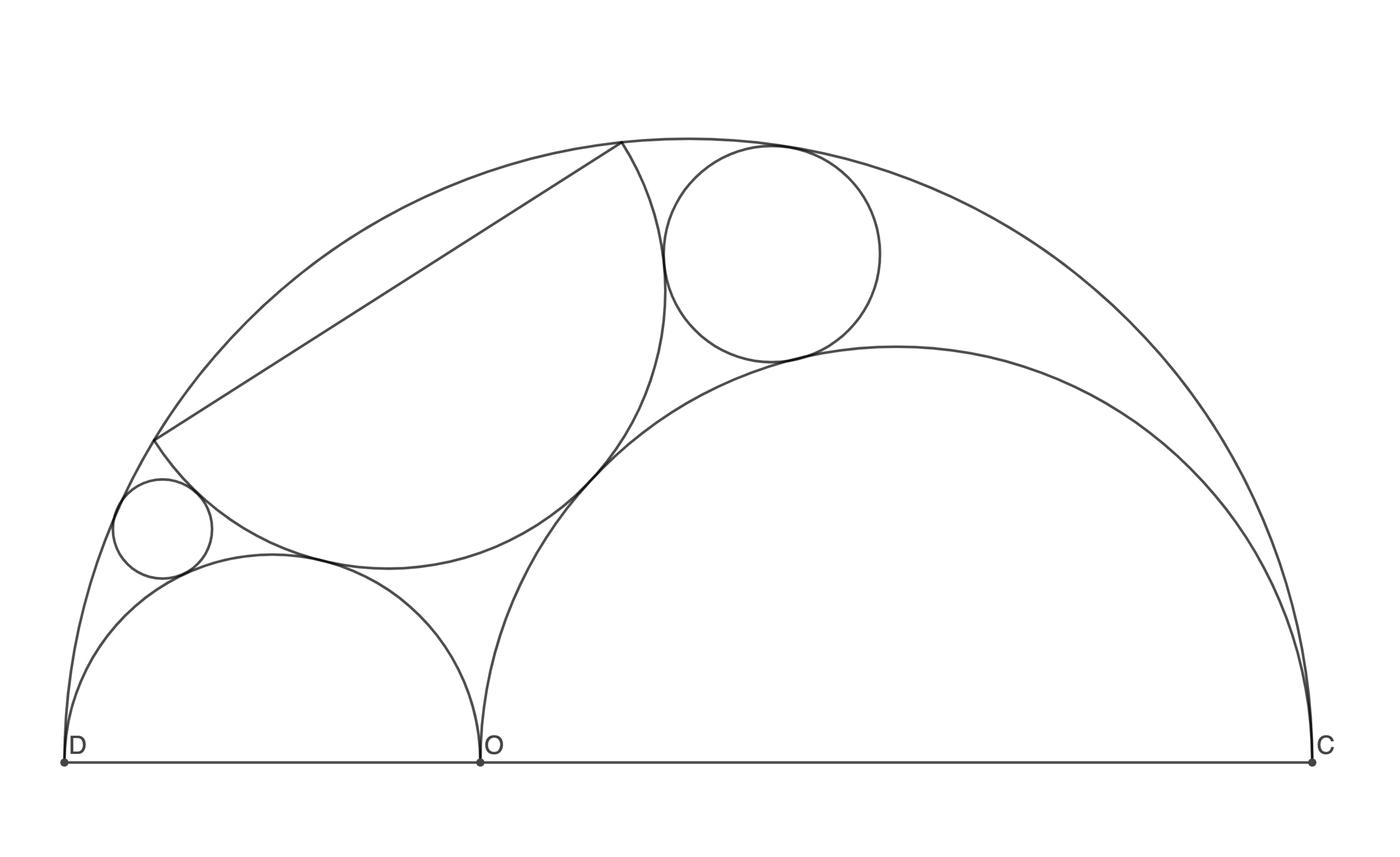
This arbelos shows three semicircles inscribed in a fourth semicircle. Two incircles to curvilinear triangles have also been inscribed. If , what is the ratio of the radius of the larger circle to the smaller circle? Express the ratio as , where and are coprime positive integers, and submit .
The answer is 159.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
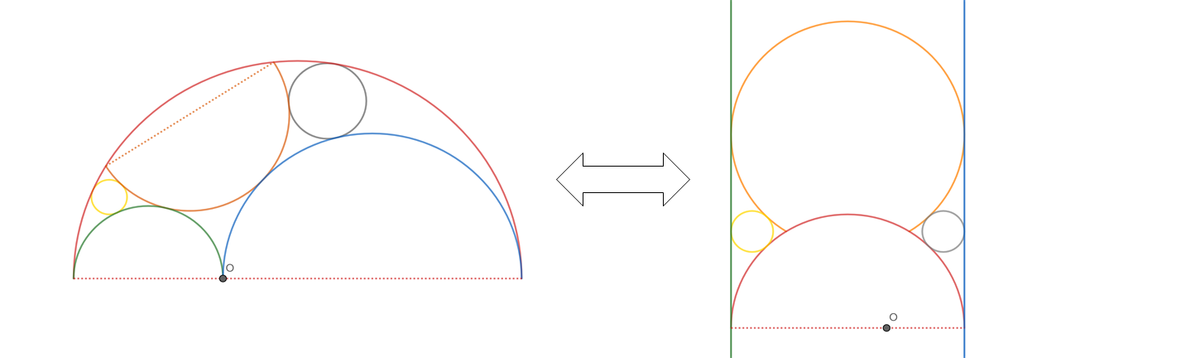
Label the diagram as follows:
Let O D = 2 and O C = 4 , so that the radius of the left semi-circle is 1 , the radius of the right semi-circle is 2 , and the radius of the large semi-circle is 3 , and D A = A O = O B = B E = 1 and E C = 2 .
Let the radius of the upside-down semi-circle be R . Then by the Pythagorean Theorem on △ K H B , K B = H B 2 − K H 2 = 9 − R 2 .
By the law of cosines on △ A K B , cos ∠ K A B = 2 ⋅ A K ⋅ A B A K 2 + A B 2 − K B 2 = 2 ⋅ ( R + 1 ) ⋅ 2 ( R + 1 ) 2 + 2 2 − ( 9 − R 2 ) = 2 ( R + 1 ) R 2 + R − 2 .
By the law of cosines on △ A K E , cos ∠ K A B = 2 ⋅ A K ⋅ A E A K 2 + A E 2 − K E 2 = 2 ⋅ ( R + 1 ) ⋅ 3 ( R + 1 ) 2 + 3 2 − ( R + 2 ) 2 = 3 ( R + 1 ) 3 − R .
Therefore, cos ∠ K A B = 2 ( R + 1 ) R 2 + R − 2 = 3 ( R + 1 ) 3 − R , which solves to R = 3 4 for R > 0 .
Since R = 3 4 , A K = 1 + 3 4 = 3 7 , K E = 2 + 3 4 = 3 1 0 , and cos ∠ K A B = 3 ( 3 4 + 1 ) 3 − 3 4 = 2 1 5 .
That means sin ∠ K A B = 1 − cos 2 ∠ K A B = 1 − ( 2 1 5 ) 2 = 2 1 4 2 6 .
By the law of cosines on △ A K E , cos ∠ K E A = 2 ⋅ K E ⋅ A E K E 2 + A E 2 − A K 2 = 2 ⋅ 3 1 0 ⋅ 3 ( 3 1 0 ) 2 + 3 2 − ( 3 7 ) 2 = 1 5 1 1 .
That means sin ∠ K E A = 1 − cos 2 ∠ K E A = 1 − ( 1 5 1 1 ) 2 = 1 5 2 2 6 .
Let the smaller circle have a radius of S . By the law of cosines on △ A F K , cos ∠ F A K = 2 ⋅ A F ⋅ A K A F 2 + A K 2 − F K 2 = 2 ⋅ ( S + 1 ) ⋅ 3 7 ( S + 1 ) 2 + ( 3 7 ) 2 − ( S + 3 4 ) 2 = 7 ( S + 1 ) 7 − S .
That means sin ∠ F A K = 1 − cos 2 ∠ F A K = 1 − 7 2 ( S + 1 ) 2 ( 7 − S ) 2 = 7 ( S + 1 ) 4 S ( 3 S + 7 ) .
So cos ∠ F A B = cos ( ∠ F A K + ∠ K A B ) = cos ∠ F A K ⋅ cos ∠ K A B − sin ∠ F A K ⋅ sin ∠ K A B = 7 ( S + 1 ) 7 − S ⋅ 2 1 5 − 7 ( S + 1 ) 4 S ( 3 S + 7 ) ⋅ 2 1 4 2 6 = 1 4 7 ( S + 1 ) 5 ( 7 − S ) − 1 6 2 6 S ( 3 S + 7 ) .
By the law of cosines on △ F A B , cos F A B = 2 ⋅ A F ⋅ A B A F 2 + A B 2 − F B 2 = 2 ⋅ ( S + 1 ) ⋅ 2 ( S + 1 ) 2 + 2 2 − ( 3 − S ) 2 = S + 1 2 S − 1 .
Therefore, cos ∠ F A B = 1 4 7 ( S + 1 ) 5 ( 7 − S ) − 1 6 2 6 S ( 3 S + 7 ) = S + 1 2 S − 1 , which solves to S = 1 0 9 2 6 .
Let the larger circle have a radius of T . By the law of cosines on △ K E L , cos ∠ K E L = 2 ⋅ E L ⋅ K E E L 2 + K E 2 − K L 2 = 2 ⋅ ( T + 2 ) ⋅ 3 1 0 ( T + 2 ) 2 + ( 3 1 0 ) 2 − ( T + 3 4 ) 2 = 5 ( T + 2 ) T + 1 0 .
That means sin ∠ K E L = 1 − cos 2 ∠ K E L = 1 − 5 2 ( T + 2 ) 2 ( T + 1 0 ) 2 = 5 ( T + 2 ) 2 2 T ( 3 T + 1 0 ) .
So cos ∠ B E L = cos ( ∠ K E A + ∠ K E L ) = cos ∠ K E A ⋅ cos ∠ K E L − sin ∠ K E A ⋅ sin ∠ K E L = 1 5 1 1 ⋅ 5 ( T + 2 ) T + 1 0 − 1 5 2 2 6 ⋅ 5 ( T + 2 ) 2 2 T ( 3 T + 1 0 ) = 7 5 ( T + 2 ) 1 1 ( T + 1 0 ) − 8 1 3 T ( 3 T + 1 0 ) .
By the law of cosines on △ B E L , cos B E L = 2 ⋅ E L ⋅ B E E L 2 + B E 2 − B L 2 = 2 ⋅ ( T + 2 ) ⋅ 1 ( T + 2 ) 2 + 1 2 − ( 3 − T ) 2 = T + 2 5 T − 2 .
Therefore, cos ∠ B E L = 7 5 ( T + 2 ) 1 1 ( T + 1 0 ) − 8 1 3 T ( 3 T + 1 0 ) = T + 2 5 T − 2 , which solves to T = 2 5 1 3 .
Therefore, the ratio of the radius of the larger circle to the smaller circle is S T = 1 0 9 2 6 2 5 1 3 = 5 0 1 0 9 , so p = 1 0 9 , q = 5 0 , and p + q = 1 5 9 .