$\arctan$ Arithmetics

By the following identity $\arctan\left(\dfrac{1}{{\color{#D61F06}a}}\right) - \arctan\left(\dfrac{1}{{\color{#3D99F6}b}}\right) = \arctan\left(\dfrac{{\color{#3D99F6}b} - {\color{#D61F06}a}}{{\color{#D61F06}a}{\color{#3D99F6}b} + 1}\right)$ if ${\color{#D61F06}a} = x$ and ${\color{#3D99F6}b} = x + 1$ , we have $\arctan\left(\dfrac{1}{x^2 + x + 1}\right) = \arctan\left(\dfrac{1}{2\left(x + 1\right)}\right)$ where equality holds if $x^2 + x + 1 = 2\left(x + 1\right)$ Simplifying, we see that $x^2 - x - 1 = 0$ , the polynomial that is famous for having the golden ratio $\dfrac{1 + \sqrt{5}}{2}$ and $\dfrac{1 - \sqrt{5}}{2}$ as the solutions. However, since $\dfrac{1 - \sqrt{5}}{2}$ doesn't satisfy the given equation, the $\boxed{\text{golden ratio}}$ is the only solution that works.

Remark : Another way to show that $\dfrac{1 - \sqrt{5}}{2}$ does not satisfy the equation is to consider the following diagram: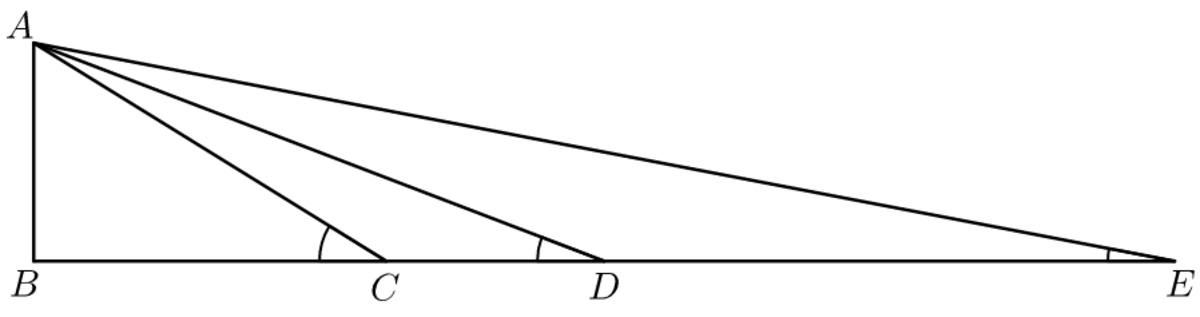 Here, $|\overline{AB}| = 1$ , $|\overline{BC}| = x$ , $|\overline{BD}| = x + 1$ and $|\overline{BE}| = 2\left( x + 1\right)$ Because $\Delta ABC$ , $\Delta ABD$ and $\Delta ABE$ all share common side $\overline{AB}$ with length $1$ , then $\angle ACB, \angle ADB$ and $\angle AEB$ are all less than $90^{\circ}$ . In this case, $x, x + 1, 2(x + 1) > 0$ . Otherwise, if $m\angle ACB \geq 90^{\circ}$ , the given equation doesn't hold.

$\begin{aligned} \arctan \frac 1x - \arctan \frac 1{x+1} & = \arctan \frac 1{2(x+1)} \\ \tan \left(\arctan \frac 1x - \arctan \frac 1{x+1}\right) & = \tan \left(\arctan \frac 1{2(x+1)}\right) \\ \frac {\frac 1x-\frac 1{x+1}}{1+\frac 1{x(x+1)}} & = \frac 1{2(x+1)} \\ \frac 1{x^2+x+1} & = \frac 1{2x+2} \\ \implies x^2 + x+1 & = 2x+2 \\ x^2 - x -1 & = 0 \\ \implies x & = \frac {1 \pm \sqrt 5}2 \end{aligned}$

$\begin{cases} x = \frac {1+\sqrt 5}2 & LHS = \arctan \frac 2{1+\sqrt 5} - \arctan \frac 2{3+\sqrt 5} \color{#3D99F6} > 0 & RHS = \arctan \frac 1{3+\sqrt 5} \color{#3D99F6} > 0 & \small \color{#3D99F6} \text{Accepted} \\ x = \frac {1-\sqrt 5}2 & LHS = \arctan \frac 2{1-\sqrt 5} - \arctan \frac 2{3-\sqrt 5} \color{#D61F06} < 0 & RHS = \arctan \frac 1{3-\sqrt 5} \color{#3D99F6} > 0 & \small \color{#D61F06} \text{Rejected} \end{cases}$

Therefore, the answer $x = \frac {1+\sqrt 5}2 \approx \boxed{1.618}$ .