Are They Comfortable?

Geometry Level 4

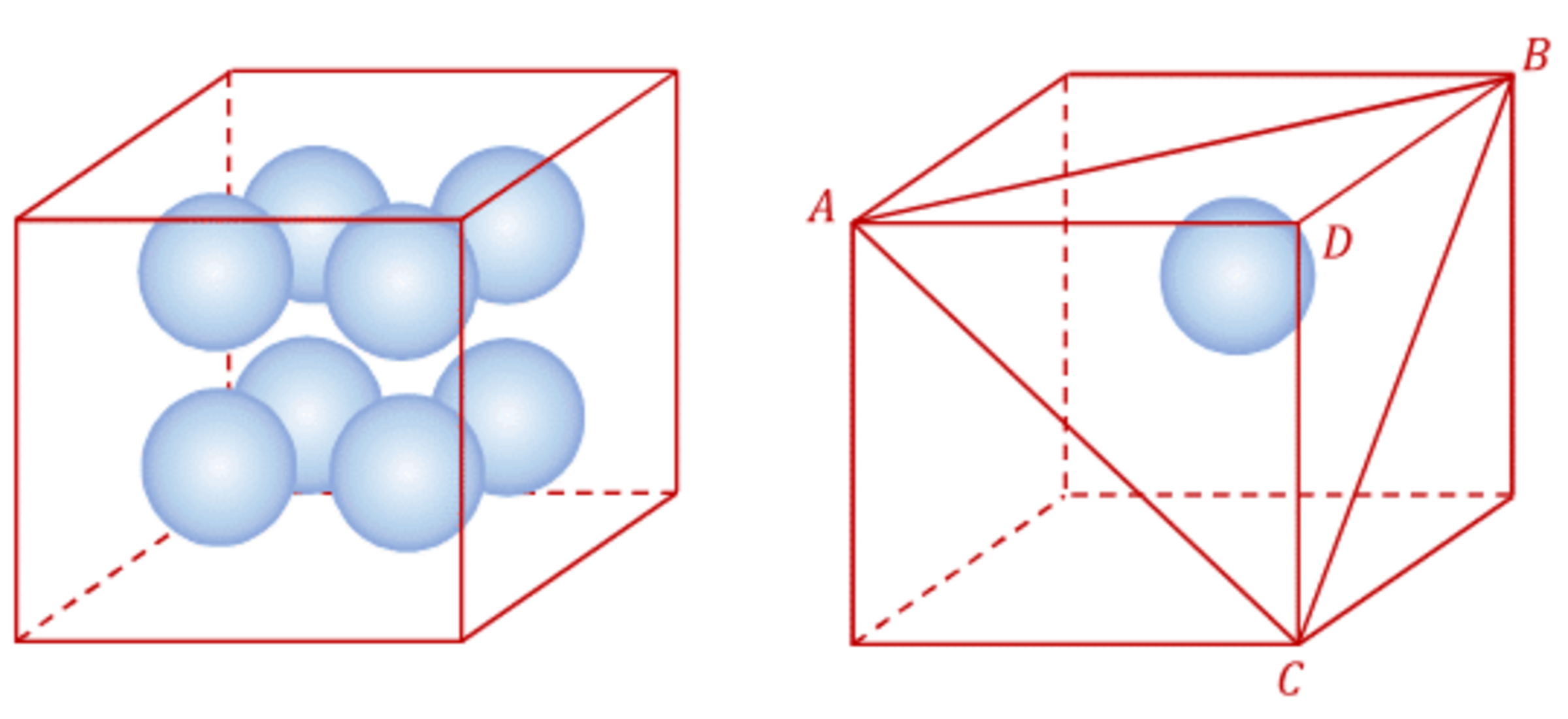
Eight spheres are crowded inside a unit cube. Each of them is inscribed into a not-quite-regular tetrahedral cap like the one pictured in the image on the right with vertices $ABCD$ .

What is the distance between the spheres?

More precisely, what is the size of the gap left between two orthogonally adjacent spheres, calculated as the distance between the centers minus twice the radius. If the spheres overlap, this "distance" will come out negative.

The answer is 0.1547.

1 solution

Marta Reece
Mar 7, 2017

Viewed from above, as in the middle image, we see that if a sphere with radius $R$ is in contact with two sides at right angles to each other, the distance from the center of the sphere to the corner, $OF$ in the image, will be $R\sqrt{2}$ .

With this established, let’s turn our attention to the triangle $CDG$ , in the cube 1n the left image and alone in the right one, and its relationship to the inscribed sphere. $DC=1, GD=\frac{1}{\sqrt{2}}, \angle CDG=90^\circ$ , therefore $CG=\sqrt{\frac{1}{2}+1}=\frac{\sqrt{3}}{\sqrt{2}}$ .

Area of this triangle is $A=\frac{1}{2}\times1\times\frac{1}{\sqrt{2}}=\frac{1}{2\sqrt{2}}$ .

On the basis of the triangles $GOD, DOC$ , and $COG$ it is also $A=\frac{1}{2}R\times\frac{1}{\sqrt{2}}+\frac{1}{2}R\sqrt{2}\times 1+\frac{1}{2}R\times\frac{\sqrt{3}}{\sqrt{2}}$ .

Setting these two expressions equal to each other, we get $R=\frac{1}{1+2+\sqrt{3}}=0.2113$ .

This gives us a distance between the spheres as $1-4\times R=0.1547$ .

For finding the inradius of things that are tangential to all sides, I often find it easier to consider it via the "area-perimeter" ratio. In the 3-D case, it would be the "volume-surface area" ratio.

Take the center of the sphere and connect it to all 4 vertices, this gives us 4 tetrahedrons, each of height $r$ and base area equal to the individual face. These volumes sum up to $\frac{1}{3} \times r \times ( \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{ \sqrt{3} } { 2}$ . that of the large tetrahedron, which has volume $\frac{1}{3} \times 1 \times \frac{1}{2} = \frac{1}{6}$ . This gives us $r = \frac{1}{ 3 + \sqrt{3}$ as desired.

Calvin Lin Staff - 4 years, 3 months ago

I did a modified version of the area-perimeter ratio for the 2D part of the solution, but did not think of doing it in 3D. Thanks for the suggestion. (Would you like me to actually change the solution?)

Marta Reece - 4 years, 3 months ago

Are They Comfortable?

The answer is 0.1547.

1 solution

0 pending reports