Are They Equal?

Geometry Level 2

In a square, we draw a semicircle on the left side.
We also draw an isosceles triangle on the right side, with its apex at the center of the semicircle.

Which has a larger area, the yellow sector or the blue sector?

Yellor sector Blue sector They are equal

2 solutions

Geoff Pilling
Oct 24, 2016

The yellow angle is $atan(2) \approx 63.4$ degrees.

So, the blue angle, by symmetry is $(180 - 2*63.4)$ degrees $\approx 53.2$ degrees.

So, the $\boxed{\text{yellow sector}}$ has a larger area since the area is proportional to the angle.

And if you prefer to do it without trigonometry...

You can see that the diagonal lines have a length greater than 2. So the triangle made up of the two diagonal lines and the right edge must have an angle on the left side less than 60 degrees. Therefore it is the smallest angle, since the other two angles must equal each other by symmetry, and the three angles must add up to 180 degrees.

Can you do it without using trigonometry?

If not, I can add my solution.

Chung Kevin - 4 years, 7 months ago

Yes. You can see that the diagonal lines have a length greater than 2. So the triangle made up of the two diagonal lines and the right edge must have an angle less than 60 degrees. Therefore it is the smallest angle, since the other two angles must equal each other by symmetry.

Geoff Pilling - 4 years, 7 months ago

Ah yes. I first started with a semicircle and an equilateral triangle, where they would yield the same area. But to get a square, we have to "lengthen" the equilateral triangle, which then reduces the angle.

So I knew it was smaller, but didn't know by how much :)

Chung Kevin - 4 years, 7 months ago

:0) Fun problem!

Geoff Pilling - 4 years, 7 months ago

Chung Kevin
Oct 27, 2016

The yellow and green sectors have the same area. If the blue sector also has the same area, then the angle would be $60 ^ \circ$ . If the angle is greater than $60 ^ \circ$ , then the area would be larger than the green sector. if the angle is less than $60 ^ \circ$ , then the area would be smaller than the yellow sector.

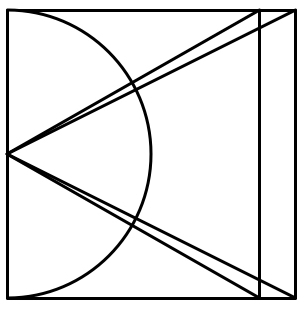
We can compare this easily by drawing in an equilateral triangle. Since the "height" of the equilateral triangle will be $\sqrt{3} < 2$ , hence we see that the angle of the blue sector is less than $60 ^ \circ$ .

Thus, the yellow sector is larger.

Nice comparison to show that it is smaller.

Calvin Lin Staff - 4 years, 7 months ago

What program do you use to make your images? Could you recommend some program?

Zuriel Aquino - 4 years, 2 months ago

I use a Mac program called Omnigraffle, which I've used for a while.

When Brilliant promotes your problem, they help improve your image and problem. They use Figma , but I'm not familiar with it.

Chung Kevin - 4 years, 2 months ago

Or another way to look at it: the lines dividing the sectors have length sqrt(5) >2. Since an equilateral triangle would have sides =2, the triangle shown is "taller" than equilateral, and the angle is less than 60 deg.

Eric Lucas - 4 years, 2 months ago

That's a good way to see it too! Similarly, calculate the height of the isosceles triangle :)

Glad that there are so many approaches from the community :)

Calvin Lin Staff - 4 years, 2 months ago

Are They Equal?

2 solutions

0 pending reports