Are they equal
The figure shows a regular grid.
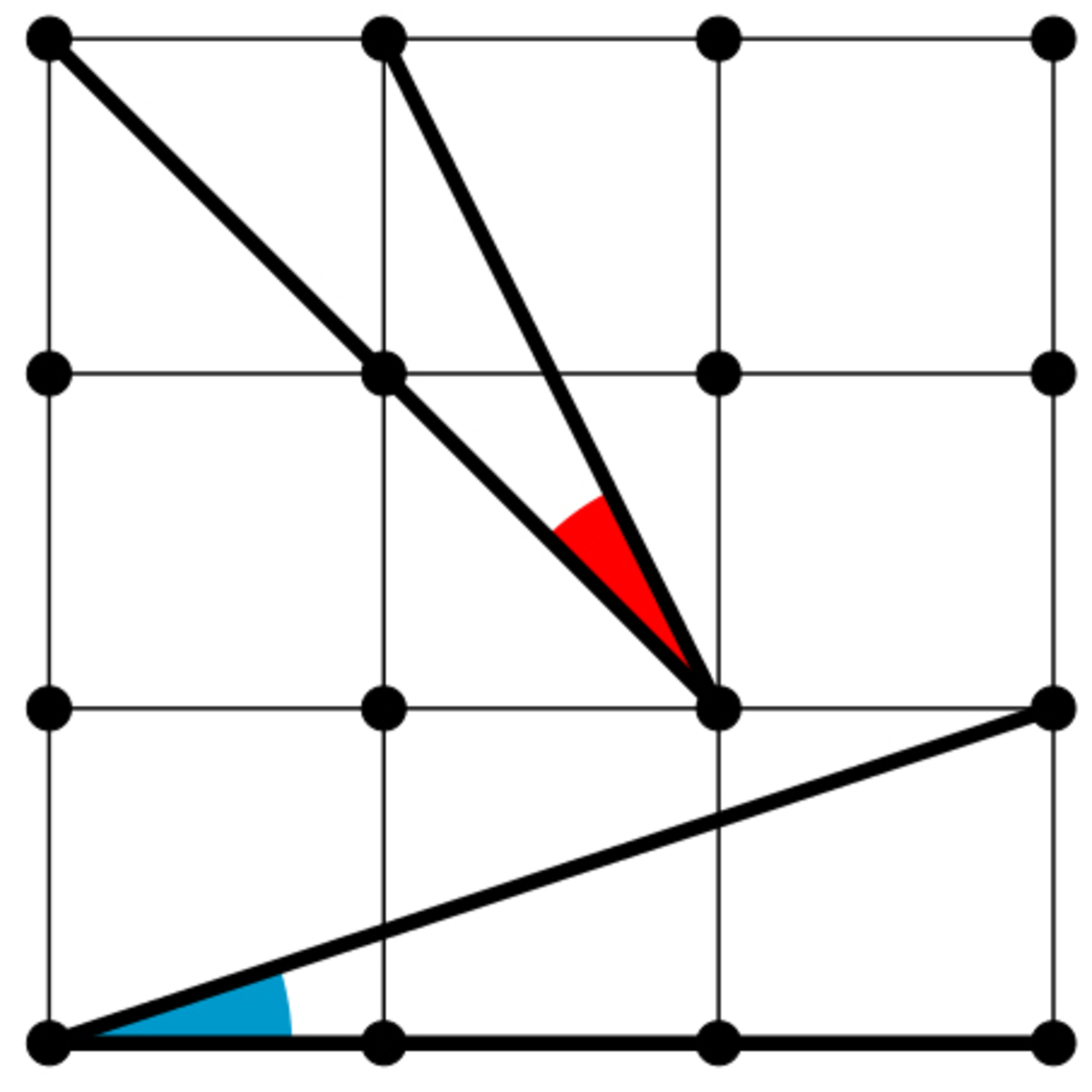
Are the colored angles equal?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We can express the blue angle as β = tan − 1 ( 3 1 )
And the red angle α as the difference between α 1 = tan − 1 1 and α 2 = tan − 1 ( 2 1 )
Since tan ( x ) is strictly increasing in the interval [ 0 , 2 π ) , we can compare tan α and tan β instead
tan α = tan ( α 1 − α 2 ) = 1 + tan α 1 ⋅ tan α 2 tan α 1 − tan α 2 = 1 + 2 1 1 − 2 1 = 3 1 = tan β
Since tan ( x ) is injective in the interval [ 0 , 2 π ) , this implies α = β
Is there a way to see this without trigo?
Log in to reply
 .
.
Yes, we just need to prove that the right triangles A B C and D E F are similar, which is fairly easy, since
A C B C = 2 3 2 2 1 2 = 3 1 = E F D E
Yes, there is! I will write a solution as soon as it is possible. (Now I'm in a camp)
Both triangles lie on two congruent circles. By the inscribed angle theorem the angles are equal.