Applying Gauss Law?
Electricity and Magnetism
Level
2
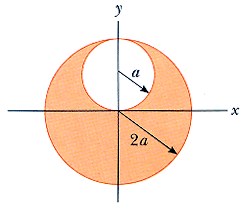
Electric Field inside a spherical cavity in a uniform solid sphere of charge
Is uniform
Is zero
Is non-uniform
Is uniform only if cavity is concentric with the sphere
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the diagram. we see that the radius of the sphere is twice the radius of the cavity. Actually, we can prove that the field is uniform regardless of how much bigger the sphere is compared to the cavity. Let b > a denote the radius of the sphere. Without loss of generality, we may assume ρ > 0 . Let E 1 be the electric field generated by a solid sphere of radius a with uniform charge density − ρ that fills the cavity, and let E 2 be the electric field generated by a solid sphere of radius b with uniform charge density ρ and no cavity. We can compute E as the superposition of E 1 and E 2 .
Suppose E 2 is centered at the origin and E 1 is centered at d , with ∣ d ∣ = d ≤ a − b . Any point inside the cavity can be written as d + r for some r with ∣ r ∣ = r < a . Consider the value of E 1 ( d + r ) . By Gauss's law, Φ = ϵ 0 Q , where Φ is the electric flux of E 1 through the spherical surface ∣ v − d ∣ = r , Q is the negative charge contained within this surface, and ϵ 0 is the electric constant. Clearly Q = − 4 π r 3 ρ / 3 . Since ∣ E 1 ∣ is the same at all points on the spherical surface, for some constant field strength E r we have Φ = E r ⋅ 4 π r 2 = − 3 ϵ 0 4 π r 3 ρ ⟹ E r = − 3 ϵ 0 r ρ . By symmetry, E 1 is radial about d , so E 1 ( d + r ) = E r ⋅ r r = − 3 ϵ 0 r ρ . Now consider the value of E 2 ( d + r ) . Applying the same reasoning we used to find E 1 ( d + r ) , we find E 2 ( d + r ) = 3 ϵ 0 ( d + r ) ρ . By superposition, E ( d + r ) = E 1 ( d + r ) + E 2 ( d + r ) = − 3 ϵ 0 r ρ + 3 ϵ 0 ( d + r ) ρ = 3 ϵ 0 d ρ . Since the value of E depends only on d , which is fixed, we have shown that E is uniform inside the cavity.