A geometry problem by Lil Phil
The area of the shaded rectangle is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I did not think of figuring out if the triangles were similar, I ended up using coordinate geometry which raised up a lot of equations. Very nice observation!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
|
Length of the shaded rectangle is 8 3 √ 5 and breadth is 4 √ 5 . Therefore it's area is 3 2 1 5 , which lies between 1 6 7 and 2 1
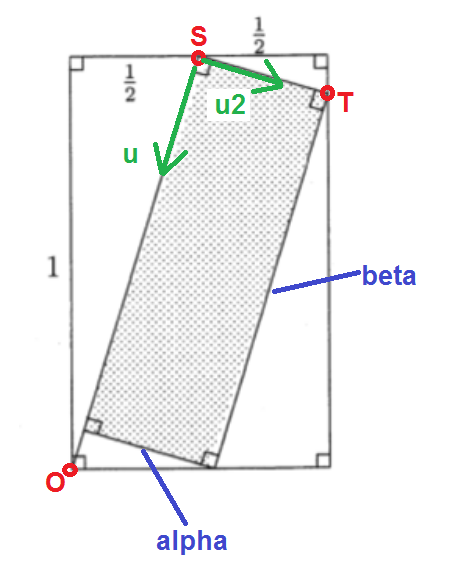
Label the outer rectangle ABCD and the inner shaded rectangle EFHG as follows:
Using angle sums of triangles and straight lines are 1 8 0 ° , it can be determined that the four white right triangles are similar by AA similarity.
From △ A E D ∼ △ B F E , B E B F = A D A E or 2 1 B F = 1 2 1 , which solves to B F = 4 1 .
By Pythagorean's Theorem on △ B F E , E F = 4 5 .
Since B F + F C = 1 and B F = 4 1 , F C = 4 3 .
From △ B F E ∼ △ C G F , F C F G = E B E F or 4 3 F G = 2 1 4 5 , which solves to F G = 8 3 5 .
The area of the shaded rectangle is then A E F G H = E F ⋅ F G = 4 5 ⋅ 8 3 5 = 3 2 1 5 , which is between 1 6 7 and 2 1 .