Are You Economical With Pizzas?
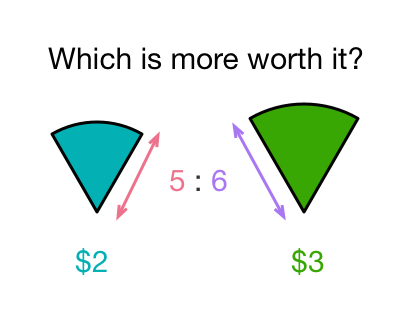
A pizza shop sells two types of triangular pizza's, one is small and costs $2 per slice while the other is large and costs $3 per slice.
Sandeep goes to buy as much as he can with $6. As Sandeep is very economical, he tries to find out which is the better option so that he can get the most area out of it.
After some research, he concludes that the ratio of each of the corresponding sides of the small pizza to the large pizza to be . Considering the given conditions, what type of pizzas should Sandeep buy?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
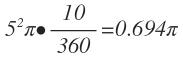
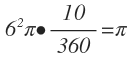
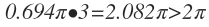
We know that the ratio of the areas of similar triangles is related to the ratio of it's sides in the following way: ar(triangle 2) ar(triangle 1) = ratio of the sides 2
Thus, the area of the small pizza to the area of the large pizza would be: ar(large pizza) ar(small pizza) = ( 6 5 ) 2 = 3 6 2 5
So, if Sandeep buys:
3 small pizzas, the resulting area would be: 3 × 2 5 x = 7 5 x .
2 large pizzas, the resulting area would be: 2 × 3 6 x = 7 2 x .
1 large and 1 small pizza, the resulting area would be: 2 5 x + 3 6 x = 6 1 x .
Thus, the most economical choice would be to buy 3 small pizzas.