My Unique Twist
We have a two digit number A B . If
( A B ) 2 = ( 2 0 × A × B ) + 4 2 5
Calculate the value of A + B
Note:-Here A B means a two digit number as oppose to multiplication A × B
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Just a mathematical way to do the last step.
If we have 4 2 5 ≡ 2 5 ( m o d 1 0 0 ) mod 100 since 100A^2 will obviously be a multiple of 100 and the last two digits of 425 will remain untouched no matter what A is. Thus we must square root 25 and are left with 5.
1 0 0 A 2 + ( 5 ) 2 = 4 2 5 ⇒ 1 0 0 A 2 = 4 0 0 ⇒ A = 2
Exactly the same!
Easy way (Trail and Error)
As we are adding 4 2 5 to the product, B should be 5 .
Now, A cannot be 1 , as 1 5 2 is 2 2 5 which is less than 4 2 5 .
Taking A as 2 , we get ( 2 5 2 ) = ( 2 0 × A × B ) + 4 2 5
Thus, A B is 2 5
(AB)^2 = (20 x A x B) +425 think a perfect square that is near in a 425 and add the product of 20 x A x B... its 525, and the square root of 525 is 25, then A=2 and B=5, so that (20 x 2 x 5) + 425 = 525... A + B = 7 2 + 5 = 7
6 2 5 = 2 5
l e t , ( 1 0 A + B ) 2 = 2 0 ∗ A ∗ B + 4 2 5 = k n o w w e o b s e r v e t h a t 2 0 ∗ A ∗ B w i l l h a v e u n i t d i g i t a s 0 s o k w i l l h a v e u n i t d i g i t 5 . s i n c e k i s a p e r f e c t s q u a r e i t s s q u a r e r o o t m u s t e n d w i t h u n i t d i g i t 5 b e c a u s e k h a s u n i t d i g i t 5 . s o B = 5 f u r t h e r s o l v e t o g e t A = 2 s o , A + B = 7
25 was literally the first number I guessed as AB and it fit as 2 was A and 5 was B and the two sides of the equation matched after solving.
If A B is a 2 digit number then we can write it as 1 0 A + B so : ( 1 0 A + B ) 2 = ( 2 0 A B ) + 4 2 5 ( 1 0 A ) 2 + 2 0 A B + B 2 = 2 0 A B + 4 2 5 ( 1 0 A ) 2 + B 2 = 4 2 5 Observe that A = 2 a n d B = 5 satisfies the equation.So sum = A + B = 2 + 5 = 7
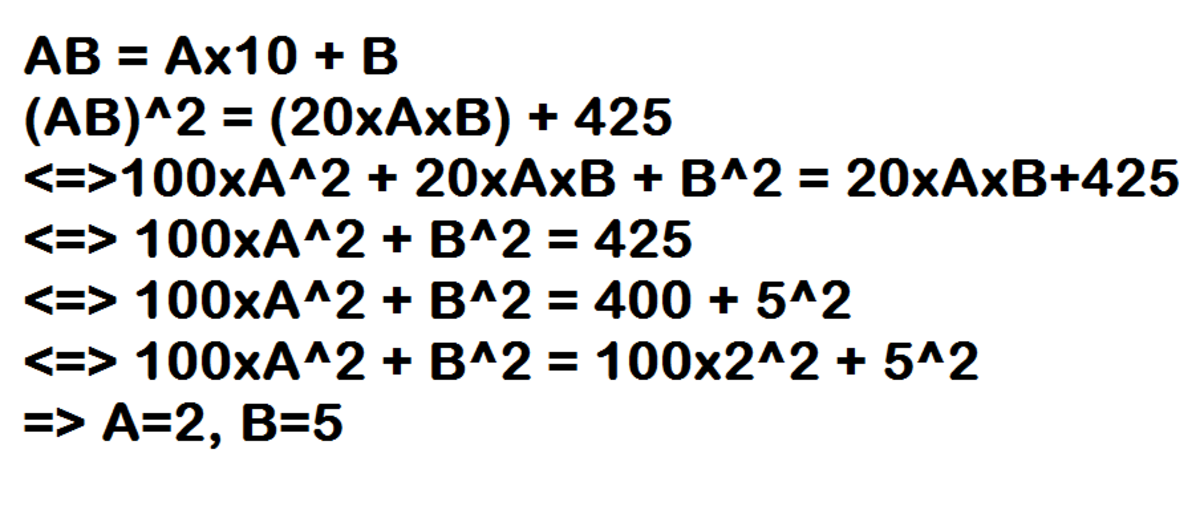
Since A B is a two digit positive integer, we can write that the value of A B = 1 0 A + B . Now, putting in the given expression, we get ----
( 1 0 A + B ) 2 = ( 2 0 × A × B ) + 4 2 5
1 0 0 A 2 + B 2 + 2 0 A B = 2 0 A B + 4 2 5
1 0 0 A 2 + B 2 = 4 2 5
We can observe that if A = 2 and B = 5 , the equation is satisfied! So, the required number = A B = 2 5
Sum of their digits = A + B = 5 + 2 = 7