Are you smarter than a 5th grader- Finale
In a convex polygon of 16 sides, find the maximum number of angles that can all be equal to 10 degrees.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
betr, But cant see how i placed 360 in place of 2520 in the inequality,A bad day is what all i can conclude
Correction: For a convex polygon, each angle ≤ 1 8 0 . Also, for the PHP part, atleast one of the non- 1 0 ∘ angles must be ≥ their average.
By the way, nice use of PHP! Upvoted. :)
Another way to solve this problem is to minimize the number of non- 1 0 ∘ angles which can be done by maximizing angle value.
The maximum value that the non- 1 0 ∘ angles can take is 1 8 0 ∘ . Also, the sum of all angles is 2 5 2 0 .
2 5 2 0 = 1 8 0 × 1 3 + 1 8 0
Now, we do casework. We cannot take any more 1 8 0 ∘ angles since then we would be 2 angles short. Now, all the three angles can't be 1 0 ∘ since that would result in 1 5 0 ∘ shortage. If we have two 1 0 ∘ angles, then the third angle would be 1 6 0 ∘ ≤ 1 8 0 ∘ . We need to find max case for 1 0 ∘ angles, so we don't have to dig any deeper. We have the required answer as 2 . It saddens me that my method relied completely on brute forcing the problem.
Let's do it the other way friends ............ We can find the angle sum of that polygon by using ( 1 6 − 2 ) ∗ 1 8 0 = 2 5 2 0
And each individual angle by considering it regular for time being as 157.5 degrees
Now the trick comes into play here ...........................
suppose we diminish one of these angles to 0 but 10 degrees then the 147.5 degrees required to complete the angle sum will be equally divided among the other 15 sides ............then diminishing the next angle to 0but 10 degree also follows the same way
now it is found that after 2 consecutive diminished angles to 10 degrees further diminishing results in concave polygon
so the answer is ...................... 2
The sum of external angles of a convex polygon has to be 3 6 0 ∘ .
A 1 0 ∘ internal angle produces a 1 7 0 ∘ external angle. Two such angles add up to 2 × 1 7 0 ∘ = 3 4 0 ∘ leaving 2 0 ∘ for the remaining 14 vertices. However three such angles add up to 3 × 1 7 0 ∘ = 5 1 0 ∘ , an impossibility.
Only a self-intersecting polygon could contain such angle combination.
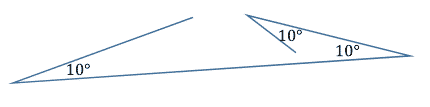
We know that the sum of interior angles=(180)n -360 where n is the number of sides.By that we get that the sum of the angles of this polygon is 2520.We know that the sum of the exterior angles of any convex polygon is 360•.So if 3 interior angles are of 10• the sum of the exterior angles would be greater than 360.So max. number of angles that can be 10 is 2.
sorry can u kindly answer this question in more detail and with the clear picture and formula
What if there were 3 exterior angles equal to 10?
suppose n angles are 10 and rest of 16-n are different from n.now the sum of angles which are not 10 is 2520-10n.now by php at least one number will be greater than their average,i.e (2520-10n)/16-n.now as the polygon is convex,each angle<180.so (2520-10n)/16-n<180 gives the bound