Are you smarter than a 5th grader- Part 2
x 1 + y 1 = 2 1
There are n ordered pairs of integers ( x , y ) to the above equation.
Input your answer as the sum of all n values of x + y .
Note: ( a , b ) is different from ( b , a ) as long as a = b
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Good job pointing out that ( 0 , 0 ) is not a solution. Even though this doesn't change the answer to this question, the answer would be different if the problem asked for the number of solutions.
Darn forgot about imputing as a sum part.
Ugh!!!!!!! Two negatives make a positive....could I have been more stupid!!! :(
what is the method to factorise
If I wanna learn, I must be smart like a child
nice factorization
Nice solution Daniel. Can you explain me why ( 0 , 0 ) is not a solution?
Log in to reply
If ( x , y ) = ( 0 , 0 ) then x 1 and y 1 don't make sense.
I actually missed the fact that ( 0 , 0 ) cannot be a solution. Thankfully it didn't affect the answer.
Doesn't Factoring Out Give (x-2)(2-y) = -4 ? Because.. I got it factored out like that and yet got 24.
(x-2)(y-2) = -4, doesn't it?
Let's look at a generalized case. Suppose we have: x 1 + y 1 = n 1 ⟹ n x + n y = x y ⟹ y ( x − n ) = n x ⟹ y = x − n n x Now note that: x − n n x = x − n n x − n 2 + n 2 = x − n n ( x − n ) + n 2 = n + x − n n 2 So we finally have: y = n + x − n n 2 So the solutions can be found from all the divisors of n 2 . In our case, n = 2 , so we have to check the factors of 4 . The rest part is easy. The sum is 2 4 .
Note: it should be kept in mind that x , y = 0 .
I had come down to y=2x/(x-2). So x-2 divides 2x. nd couldnt proceed furthur.Shouldhv occurd dat +4-4 in numerator could help bringing an integer in place of 2x. Isnt there a less trickier way???
Log in to reply
Can you see, it means (x-2) divides 4, so x-2 must belong to {-4,-2,-1,1,2,4}. which means x={-2,0,1,3,4,6}. Note that x=0 is not a solution, so we are left with only 5 choice for x, and corresponding 5 choices of y. :)
[This is not a solution.]
The question previously stated x 1 + y 1 = 2 , which has a correct answer of 2. Those who previously entered 2 were marked correct.
The problem has since been updated to x 1 + y 1 = 2 1 .
Surprisingly, there are quite some solutions that actually multiply the equation by x y . This does not seem necessary. First of all we may assume that x ≥ y and see what happens. We notice that x > 0 has to hold, since otherwise x 1 + y 1 . Also x < 5 has to hold because of our first assumption. We can now simply check all four possible values for x and find solutions for x = 1 , 3 , 4 , namely ( 1 , − 2 ) , ( 3 , 6 ) , ( 4 , 4 ) . Since the assumption x ≥ y wasn't present in the original question, we also have the reverses of these as solutions, so all solutions are { ( 4 , 4 ) , ( 3 , 6 ) , ( 6 , 3 ) , ( 1 , − 2 ) , ( − 2 , 1 ) } . The sum of all occuring values is 24.
After we multiply out and factor to reach ( x − 2 ) ( y − 2 ) = 4 , we notice that there are 3 positive pairs of solutions for x − 2 and y − 2 , and 3 negative pairs of solutions. Note that these sum to 0. Thus, we need to add the extra dded two in each number in each pair to reach the answer, which is 2 ∗ 2 ∗ 6 = 2 4
Let's say x < y. Then, we know that in order for them to sum to 1/2, 1/x must be greater than a quarter, and 1/y must be less than a quarter.
But there are limited options for 1/x > 1/4, as x can only be 3, 2, and 1. For these values of x, only only solution works, giving the answer x = 3, y = 6. This can be reversed, giving y = 6 and x = 3.
There is also the obvious positive solution of 1/4 and 1/4, but this cannot be reversed.
Hence, all the positive solutions sum to 6 + 6 + 3 + 3 + 4 + 4 = 26.
Now onto the negative solutions.
We can instantly see that one of the fractions has to be positive, and the other negative. Let's say that 1/x is positive, and 1/y is negative.
We know that 1/x must be greater than 1/2. But in order for 1/x to be greater than 1/2, x can only be 1.
This gives the solutions, x =1, y = -2, which can also be reversed to give x=-2, y =1.
The sum of the negative solutions is -2, and the sum of the positive solutions is 26.
26 - 2 = 24
Utilizing the common denominator we have
2x + 2y = xy
(with the assumption of x,y different from zero).
Then we solve that equation in y, so
y = 2x/(x-2) = 2 + 4/(x-2)
(With x different from 2, but it does not make any difference since it is easy to see that x = 2 is not a solution for the first equation).
So, for y to be an integer, it must be that
(x-2)|4
And since the divisors of 4 are 1, 2 ,4, -1, -2, -4 we have:
x - 2 = 1 -> x = 3 -> y = 6 -> A(3,6)
x - 2 = 2 -> x = 4 -> y = 4 -> B(4,4)
x - 2 = 4 -> x = 6 -> y = 3 -> C(6,3)
x - 2 = -1-> x = 1 -> y = -2-> D(1,-2)
x - 2 = -2-> x = 0 not acceptable
x - 2 = -4-> x = -2 -> y = 1-> E(-2,1).
In conclusion:
2 (3+6) + 2 (1-2) + (4+4) = 24.
My brain must be different than most on here. I attempt problems intuitively when others solve them algebraically, and I attempt them algebraically when others solve them intuitively. I avoided simplifying the equation as it was quite simple to begin with.
I knew the obvious ordered pairs of (4,4), (3,6) and (6,3) and only looked at what may be missing. If you made x be too big, say just 10, there's no integer for y to get the sum close to 1/2. 7 is too big for x. The ordered pairs I've already listed take care of all the positive ordered pairs. Now what happens if I drop a negative into the mix. Oh, (1,-2) and (-2,1) work too. Anything else...(brain scanning and scanning). Nope. Done.
(-2, 1), (1, -2), (3, 6), (4, 4), (6, 3) for - 2 + 1 + 1 - 2 + 3 + 6 + 4 + 4 + 6 + 3 = 24
x 1 + y 1 = 2 1 , for x = 0 and y = 0
⇒ x 1 = 2 1 − y 1
⇒ x 1 = 2 ⋅ y y − 2
⇒ x = y − 2 2 ⋅ y ∈ Z Hence, ( y − 2 ) ∣ 2 ⋅ y
⇒ y − 2 2 ⋅ y − 4 + 4 ∈ Z
⇒ y − 2 2 ⋅ ( y − 2 ) + 4 ∈ Z
⇒ 2 + y − 2 4 ∈ Z Thus ( y − 2 ) ∣ 4 , then
( y − 2 ) ∈ { − 4 , − 2 , − 1 , 1 , 2 , 4 }
So, y ∈ { − 2 , 0 , 1 , 3 , 4 , 6 } And for those values of y we get the pairs:
( x , y ) = { ( 1 , − 2 ) , ( 0 , 0 ) , ( − 2 , 1 ) , ( 6 , 3 ) , ( 4 , 4 ) , ( 3 , 6 ) } But we have to reconsider the pairs since we have the restriction that x = 0 and y = 0 , So..
( x , y ) = { ( 1 , − 2 ) , ( − 2 , 1 ) , ( 6 , 3 ) , ( 4 , 4 ) , ( 3 , 6 ) }
Now adding those numbers is a piece of cake!!!
Just wanted to point out that to me the SUM of the solutuions is a pair, namely
(
1
2
,
1
2
)
I solved this way . Since the role of the
x
and
y
are symmetrical we can think
x
≤
y
and we will remember to double the solutions we find changing the first with the second coordinate.
That said, let's notice that neither x nor y can be 0 , otherwise the equation has no meaning.
Second, x and y cannot be both negative otherwise the sum of their reciprocal is negative and can't be 2 1 .
So if one of them is negative the other must be positive. This means y > 0 .
If x is negative we have
y 1 = 2 1 − x 1 > 2 1
And than means y < 2 . Being an integer between 0 < y < 2 it means that (when x < 0 ) necessarily y = 1 . Substituing in the equation we get also x = − 2 . So ( − 2 , 1 ) is our first solution.
If x > 0 we first notice that neither x nor y can be 1 , otherwise the sum of their reciprocal is strictly greater than 1 . For the same reason neither x nor y can be 2 , otherwise the sum of their reciprocal is strictly greater than 2 1 .
So (in particular) we get x ≥ 3 .
On the other hand, x can't be greater than 4 otherwise, also y is greater than 4 and the sum of their reciprocal is strictly lower than 2 1 .
We have only two values possible for x . Namely x = 3 and x = 4 . Substituting in the equation we find two solutions ( 3 , 6 ) and ( 4 , 4 ) .
Doubling the solutions we get this list of possible pairs
( − 2 , 1 ) ( 1 , − 2 ) ( 3 , 6 ) ( 6 , 3 ) ( 4 , 4 )
x 1 + y 1 = 2 1
x y x + y = 2 1
2x+2y=xy
Now, to solve for x, get all the x terms on one side by subtracting 2x from each side: 2y=xy-2x
Factor the x, so as to get the x's all in one place: 2y=x(y-2)
Divide both sides by (y-2):
y − 2 2 y =x
Thereafter substituting values to y we find that the expression has an integral value only for 1,-2,3,6 and 4.
The corresponding values of x are -2,1,6,3 and 4.
Hence the sum of all the values is 24
How did you make your LaTeX appear so tiny?
I don't know! It just appeared so small!!
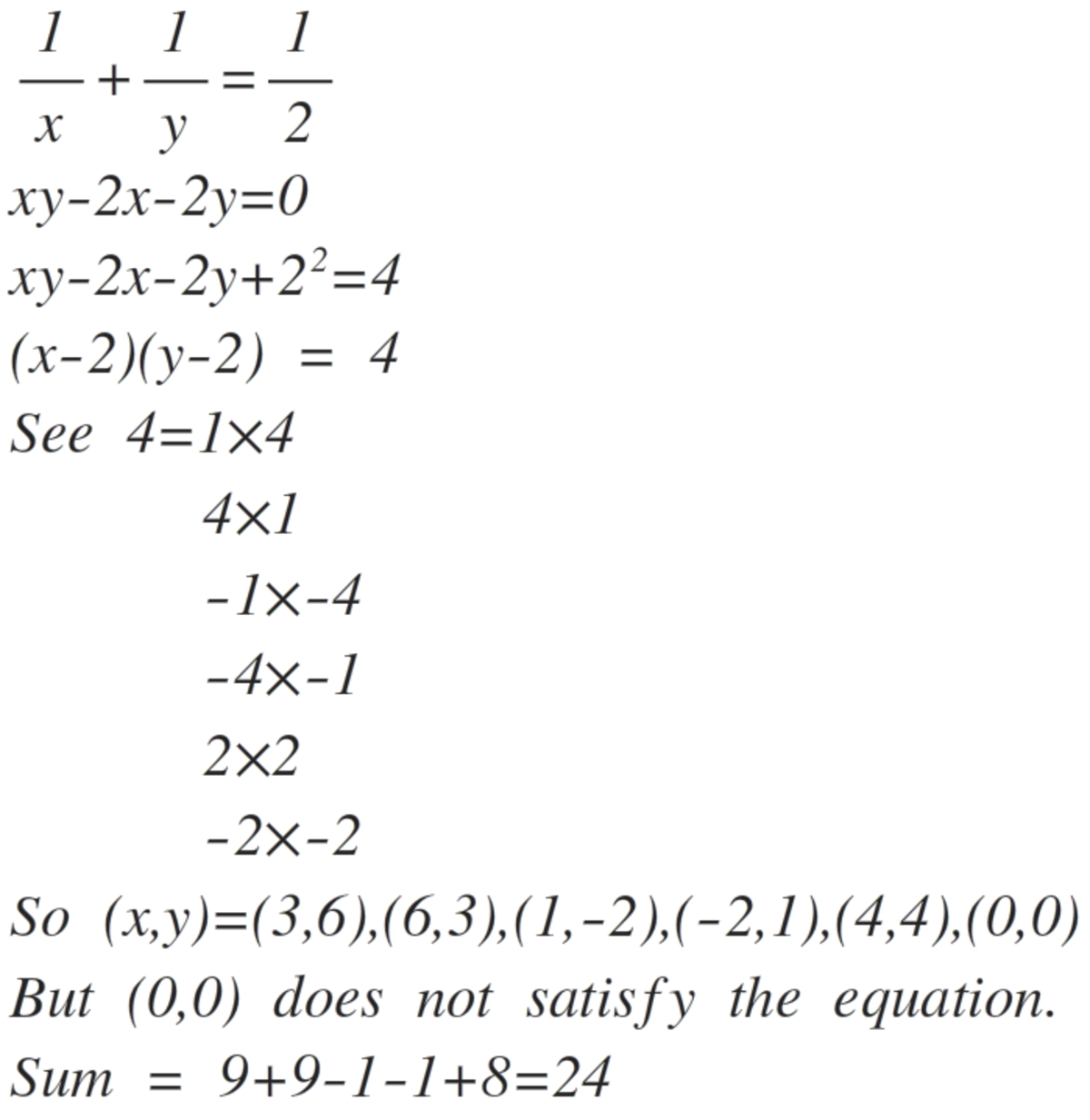
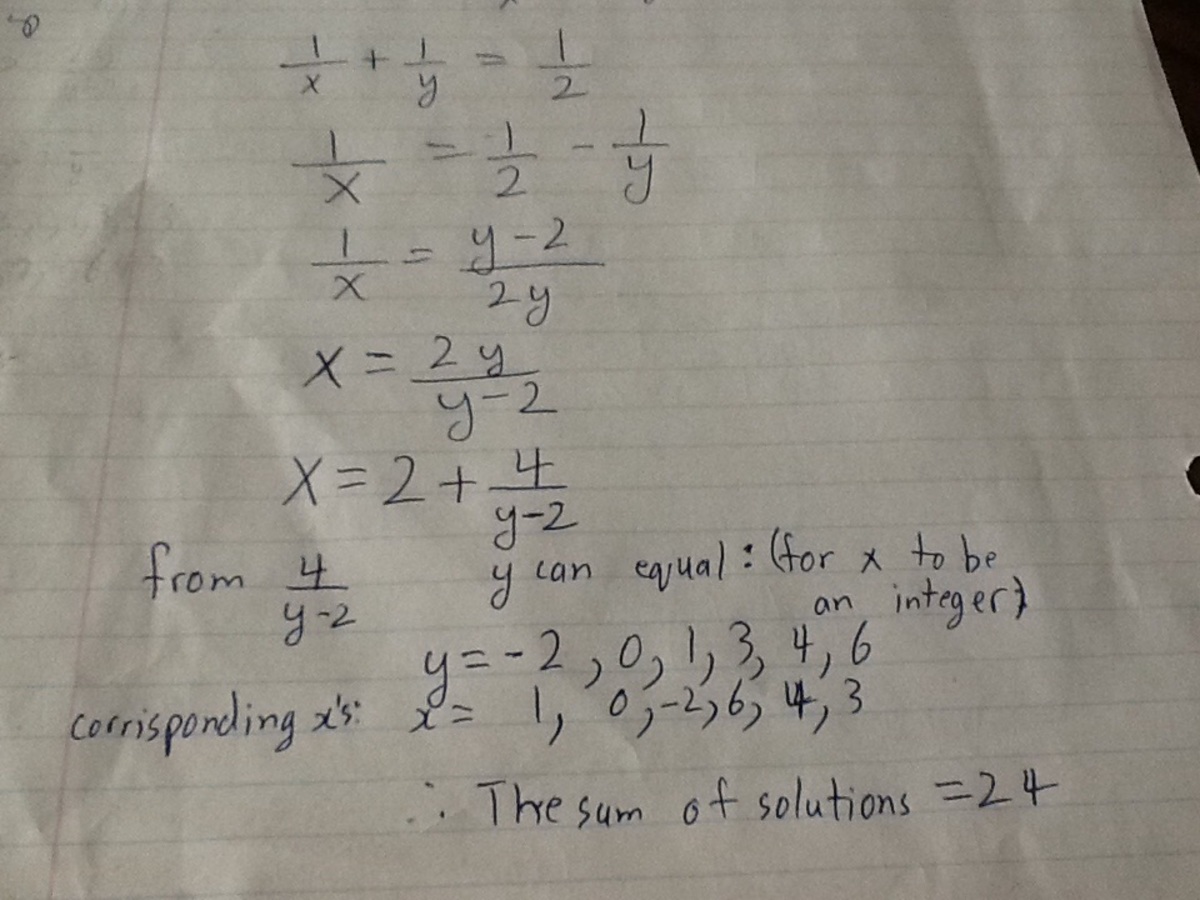
We have x 1 + y 1 = 2 1
Clearing denominators gives x y = 2 x + 2 y
Factoring gives ( x − 2 ) ( y − 2 ) = 4
Since 4 has 3 factors, we have three positive solutions for ( x , y ) :
x − 2 = 1 , y − 2 = 4 ⟹ x = 3 , y = 6 x − 2 = 2 , y − 2 = 2 ⟹ x = 4 , y = 4 x − 2 = 4 , y − 2 = 1 ⟹ x = 6 , y = 3
However, x − 2 , y − 2 can also be negative. So we double the number of solutions to get 6 total solutions:
x − 2 = − 1 , y − 2 = − 4 ⟹ x = 1 , y = − 2 x − 2 = − 2 , y − 2 = − 2 ⟹ x = 0 , y = 0 x − 2 = − 4 , y − 2 = − 1 ⟹ x = − 2 , y = 1
However, ( 0 , 0 ) does not count, so we only have 5 solutions.
If we sum the possible solutions, we arrive at 2 4 .