Circle in a trapezium
A circle is inscribed inside a trapezium A B C D such that it touches all 4 sides of this trapezium, as shown above.
Given that the area of this trapezium is 4 and the diameter of the circle is 1, find the value of the ratio C D A B .
Give your answer to 2 decimal places.
Clarification : A B is longer than C D .
The answer is 13.93.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Using Pitot's Theorem, we get the value of CB directly . This greatly minimises the usage of extra variables.
The line CP is parallel to AD not AB - otherwise great work!
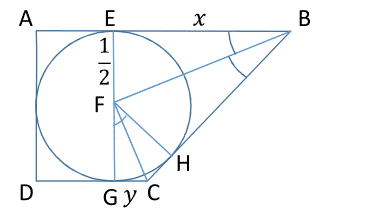
Triangles △ E B F and △ G F C are similar, therefore 1 / 2 x = y 1 / 2 giving us x = 4 y 1 . The area of the trapezoid can be composed of one rectangle and four triangles and written as
A = 2 1 + 2 1 × x + 2 1 × y = 4
Substituting for x , we get a quadratic equation in y
4 y 2 − 2 8 y + 1 = 0 with solutions y 1 = 2 1 ( 7 + 4 3 ) and y 2 = 2 1 ( 7 − 4 3 )
Interestingly enough x 1 = 4 y 1 1 = y 2 and x 2 = 4 y 2 1 = y 1 . Taking the larger one of the two values as x , in accordance with the drawing, we get the final ratio as
y + 2 1 x + 2 1
Quadrilateral POFB is similar to quadrilateral OQCF, so 0.5/x = y/0.5, or xy=1/4. Area = (1+x+y) (0.5) = 4. We have x+ y – 7 = 0, or x + 1/(4x) – 7 = 0.The quadratics eqs. 4x^2 – 28x +1=0, the solution x=0.0359, and y=6.9641. Then AB/CD = (0.5+y)/(0.5+X) = 13.93
Let M denote the intersection point between the circle and the side A B .
Let E denote the intersection point between the circle and the side C D .
Let F denote the intersection point between the circle and the side B C .
Denote x and y as the distance E C and M B , respectively.
We straight a straight line from C such that it is parallel to A B and it intersects A B at a point P .
Then, M P = E C = x .
Because the circle is tangent to both the sides A B and C B , then M B = C B = y .
Since the E M = 1 represents the diameter of the inscribed circle, and it is parallel to A D , then A D = 1 .
And A M = D E = 2 1 can be found be comparing them to the radius of the circle.
We are given that the area of the trapezium is 4, then
4 8 x + y = = = = 2 1 ( sum of lengths of the two parallel sides ) × A D = 2 1 ( A B + C D ) ( A M + M B ) + ( D E + E C ) ( 2 1 + y ) + ( 2 1 + x ) 7 ( 1 )
And because the triangle C P B is a right triangle, then by Pythagorean theorem ,
( C P ) 2 + ( P B ) 2 1 2 + ( y − x ) 2 4 x y = = = ( C B ) 2 ( y + x ) 2 1 ( 2 )
By Vieta's formula , x and y satisfy the equation z 2 − 7 z + 4 1 = 0 . Applying the quadratic formula gives
( x , y ) = ( 2 7 ± 2 3 , 2 7 ∓ 2 3 ) .
And so, we can find our ratio C D A B to be C D A B = D E + E C A M + M B = 2 1 + x 2 1 + y = 7 ± 4 3 .
But since A B > C D , then C D A B > 1 , so C D A B = 7 − 4 3 cannot be a solution.
Hence C D A B = 7 + 4 3 ≈ 1 3 . 9 3 only.