A big challenge
2 x 2 − 4 2 x + 1 6 2 x − 4 2 + 2 x 2 − 3 2 x + 9 2 x − 3 2 = 0
If the real value of x which satisfies the equation above can be expressed as c a b , find a + b + c .
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The question can be rewritten as:
d x d ( x 2 − 4 2 x + 1 6 + x 2 − 3 2 x + 9 ) = 0
So let f ( x ) = x 2 − 4 2 x + 1 6 + x 2 − 3 2 x + 9 .
Consider,
f
(
x
)
=
2
1
(
(
x
−
4
2
)
2
+
(
x
−
0
)
2
+
(
x
−
3
2
)
2
+
(
x
−
0
)
2
)
Interpreting it geometrically, we can write f ( x ) as 2 1 times the sum of distances from a point on the line y = x from ( 3 2 , 0 ) and ( 4 2 , 0 ) . So the question now transforms into finding the abscissa of the point on the line y = x whose sum of distances from the above points is minimum. i.e, derivative is zero.
There is a neat trick for such a problem. Reflect one of the points in the given line. Then draw the line joining the reflected point and the other point and find the intersection with the given line. The point of intersection is the required answer. Thus reflection of ( 4 2 , 0 ) in the line y = x is ( 0 , 4 2 ) . Hence the equation of the line is 4 x + 3 y = 1 2 2 and its intersection with y = x can be easily found giving the answer x = 7 1 2 2 and thereby the required values of a , b and c .
I found this method better because it is not as algebraically exhaustive as the other one and also a bit short and also does not yield the extraneous answer which is encountered due to squaring,
"Let's do geometric !
Let E = x 2 − 4 2 x + 1 6 + x 2 − 3 2 x + 9 .
And we have Given That : d x d E = 0 . So 'E' should be Minimum (Since Maximum value is clearly ∞ )
Now Inter-prate that This expression is written in form of cosine law . According to figure :
 Figure
Figure
E = AD + DC and By Triangle inequality in Triangle ADC : A D + D C ≥ A C .
And For calculating AC note that Triangle ABC is right angled triangle. So By Pythogoras Theoram : A C = 5 . E m i n = A m i n = 5 . "
For Calculating Value of 'x' Let's Redraw the diagram , Now 'D' must lies on AC for to minimizes The given expression (Condition for Triangle equality )
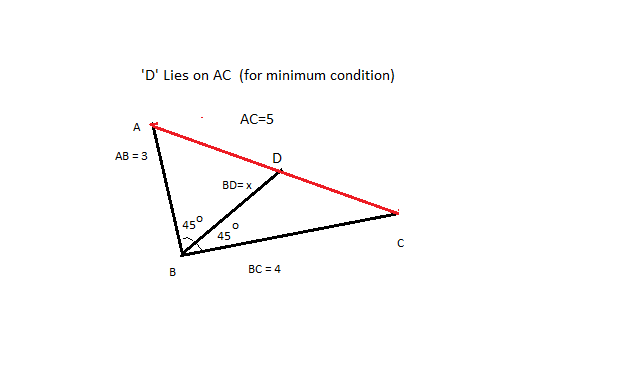
A r e a ( Δ A D B ) + A r e a ( Δ C D B ) = A r e a ( Δ A B C ) 2 1 ( 4 x ) sin ( 4 5 ) + 2 1 ( 3 x ) sin ( 4 5 ) = 2 1 ( 4 ) ( 3 ) sin ( 9 0 ) x = 7 1 2 2 .
F ( n ) = 2 x 2 − n 2 x + n 2 2 x − n 2 re -arrange and F ( n ) = 2 x 2 − 2 n 2 x + 2 n 2 x 2 − n F ( 3 ) 2 = F ( 4 ) 2 2 x 2 + 1 8 − 6 x 2 2 x 2 − 6 x 2 + 9 = 2 x 2 + 3 2 − 8 x 2 2 x 2 − 8 x 2 + 1 6 1 − 2 x 2 + 1 8 − 6 x 2 9 = 1 − 2 x 2 + 3 2 − 8 x 2 1 6 2 x 2 + 1 8 − 6 x 2 9 = 2 x 2 + 3 2 − 8 x 2 1 6 1 8 x 2 + 2 8 8 − 7 2 x 2 = 3 2 x 2 + 2 8 8 − 9 6 x 2 1 4 x 2 − 2 4 x 2 = 0 x = 7 1 2 2 o r 0 ( r e j e c t e d ) and 1 2 + 2 + 7 = 2 1
2 x 2 − 4 2 x + 1 6 2 x − 4 2 + 2 x 2 − 3 2 x + 9 2 x − 3 2 = 0
⇒ 2 x 2 − 4 2 x + 1 6 2 x − 4 2 = − 2 x 2 − 3 2 x + 9 2 x − 3 2
Squaring both sides:
4 ( x 2 − 4 2 x + 1 6 ) 4 x 2 − 1 6 2 x + 3 2 = 4 ( x 2 − 3 2 x + 9 ) 4 x 2 − 1 2 2 x + 1 8
Dividing nominator and denominator of both sides by 4 :
x 2 − 4 2 x + 1 6 x 2 − 4 2 x + 8 = x 2 − 3 2 x + 9 x 2 − 3 2 x + 2 9
⇒ x 2 − 4 2 x + 1 6 x 2 − 4 2 x + 1 6 − 8 = x 2 − 3 2 x + 9 x 2 − 3 2 x + 9 − 2 9
⇒ 1 − x 2 − 4 2 x + 1 6 8 = 1 − x 2 − 3 2 x + 9 2 9
⇒ x 2 − 4 2 x + 1 6 8 = x 2 − 3 2 x + 9 2 9
⇒ 1 6 ( x 2 − 3 2 x + 9 ) = 9 ( x 2 − 4 2 x + 1 6 )
⇒ 7 x 2 − 1 2 2 x = 0 ⇒ x = 0 or x = 7 1 2 2
⇒ a = 1 2 , b = 2 and c = 7 ⇒ a + b + c = 1 2 + 2 + 7 = 2 1