Third or Sixth Root Unity?
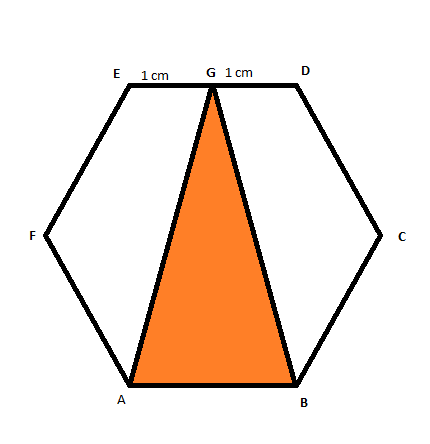 A
B
C
D
E
F
is a regular hexagon with each side of
2
cm
. Then find the area of the
△
A
B
G
to four decimal places.
A
B
C
D
E
F
is a regular hexagon with each side of
2
cm
. Then find the area of the
△
A
B
G
to four decimal places.
The answer is 3.4641.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
I just calculated the apothem and used the traditional triangle area formula.
Look at the figure below:
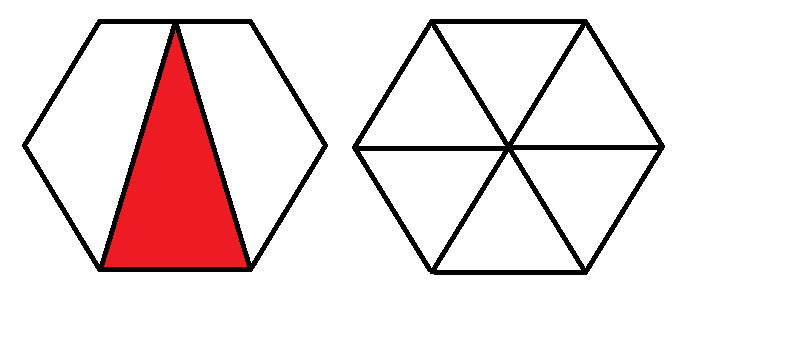 In the figure is the hexagon
A
B
C
D
E
F
and in the second figure it is also divided into 6 equilateral triangles.The height of the equilateral triangles divides them into 2 right triangles with base 1 cm and hypotenuse 2 cm.Therefore by the Pythagorean theorem we get:
(
H
e
i
g
h
t
)
2
+
1
2
=
2
2
(
H
e
i
g
h
t
)
2
=
4
−
1
=
3
H
e
i
g
h
t
=
3
In the figure is the hexagon
A
B
C
D
E
F
and in the second figure it is also divided into 6 equilateral triangles.The height of the equilateral triangles divides them into 2 right triangles with base 1 cm and hypotenuse 2 cm.Therefore by the Pythagorean theorem we get:
(
H
e
i
g
h
t
)
2
+
1
2
=
2
2
(
H
e
i
g
h
t
)
2
=
4
−
1
=
3
H
e
i
g
h
t
=
3
The height of the equilateral triangles is half the height of A B G .So the height of A B G is 2 × 3 = 2 3 .The base of A B G is 2cm so: A r e a = 2 1 × b r e a d t h × h e i g h t = 2 1 × 2 × 2 3 = 2 3 = 3 . 4 6 4 T o 4 d e c i m a l p l a c e s
Isn't the upload image feature great
Very easy simply adding the points A,E and B,D then we get ∆ ABG=(1/2)* rectangle ABDE . Again it is very simple that the height of the triangle is a√3 so the area of the triangle is (1/2) a a√3 sq unit so ar(∆ ABG)=3.4641 sq cm. Can't be it done like it!!!!!!!!!!
 In
△
B
C
D
−
In
△
B
C
D
−
By sine rule,
sin 1 2 0 B D = sin 3 0 B C
B D = 4 × sin 1 2 0
Area of Shaded △ = 2 1 × D E × B D
= 2 1 × 2 × 4 × sin 1 2 0
= 4 × 0 . 8 6 6
= 3 . 4 6 4
Did the same thing.
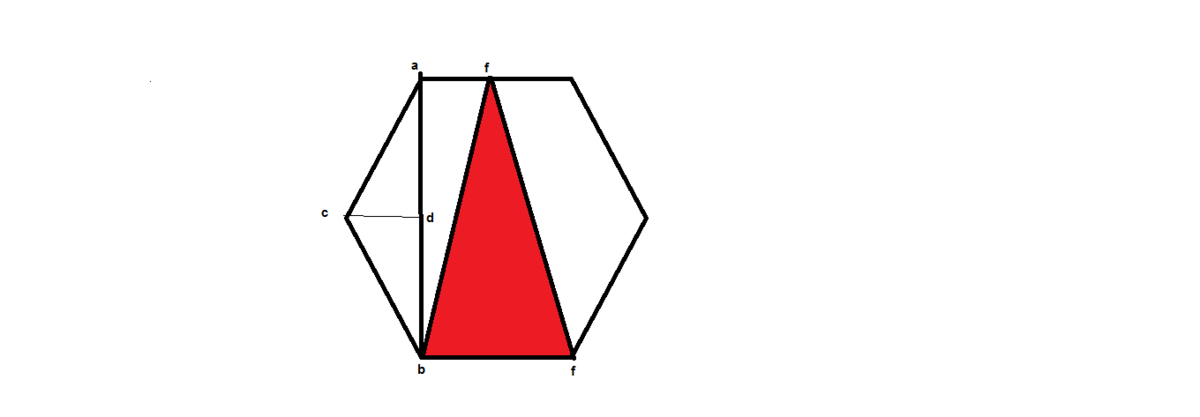 C
D
=
A
E
=
1
,
A
B
=
2
A
D
=
2
A
C
2
−
A
D
2
=
2
3
∆
A
E
F
=
2
1
×
A
B
×
B
F
=
2
1
×
2
3
×
2
=
2
3
=
3
.
4
6
4
C
D
=
A
E
=
1
,
A
B
=
2
A
D
=
2
A
C
2
−
A
D
2
=
2
3
∆
A
E
F
=
2
1
×
A
B
×
B
F
=
2
1
×
2
3
×
2
=
2
3
=
3
.
4
6
4
The apothem is calculated with the formula sqrt(side^2 - (side/2)^2)
sqrt(2^2 - (2/2)^2) = sqrt(3)
The height of the triangule is 2 * apothem => 2 sqrt(3)
The area of a triangle is calculated with the formula (base * height)/2
=> 2*2sqrt(3)/2 = 2 sqrt(3)
Ans: 2 sqrt(3)
Area of ABG = 1/2(AB)(h) join E and A and h=EA such that angle F meets EA at O, F is divided in two angles F= EFO+AFO=120 (Hexagon's angle) EFO=30 and AFO=90 EO=FE Cos30 , OA= FA Cos30 EO=2(0.866), OA=2(0.866) EO=1.732, OA=1.732 EA=EO+OA EA=3.464 A=1/2(h)(AB) A=1/2(3.464)(2) A=3.464 sq cm
A=1/2 bh; a=1cot 30=sqrt3 and h=2a Substituting, A=1/2 x 2 x 2sqrt3 =2x sqrt3=3.464sqcm.
Area of △ A B G = 2 1 × A B × A E = 2 1 × 2 × 2 × A F × cos 3 0 ∘
= 2 1 × 2 × 2 × 2 × 2 3 = 2 3 = 3 . 4 6 4