Are you smarter than me? 39
If a is a root of x 2 − 3 x + 1 .Then If the value of a 6 + 1 a 3 can be expressed as β α .Find α + β
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Nice and elegant.
very nice solution sir
Please explain that how our answer is right if we reciprocal the equation as you have done in first line .
My Solution.. :) . . .
If you don't see it clearly, then, here's the solution:
Since A is a root of x^2-3x+1=0,then we can say that a^2-3a+1 is also=to zero.
So,a^3/(a^6+1)=a^3/(a^2+1)(a^4-a^2+1)
Since a^2-3a+1=0→a^2+1=3a ;3a-1=a^2→9a^2-6a+1=a^4
=a^3/(3a)(9a^2-6a+1-(3a-1)+1)
=a^2/(3)(9a^2-9a+3)
=a^2/(9)(3a^2-3a+1)
=a^2/(9)(3a^2-a^2 )
=a^2/(9)(2a^2 )
=1/18
∴ α+β=1+18=19 ∎
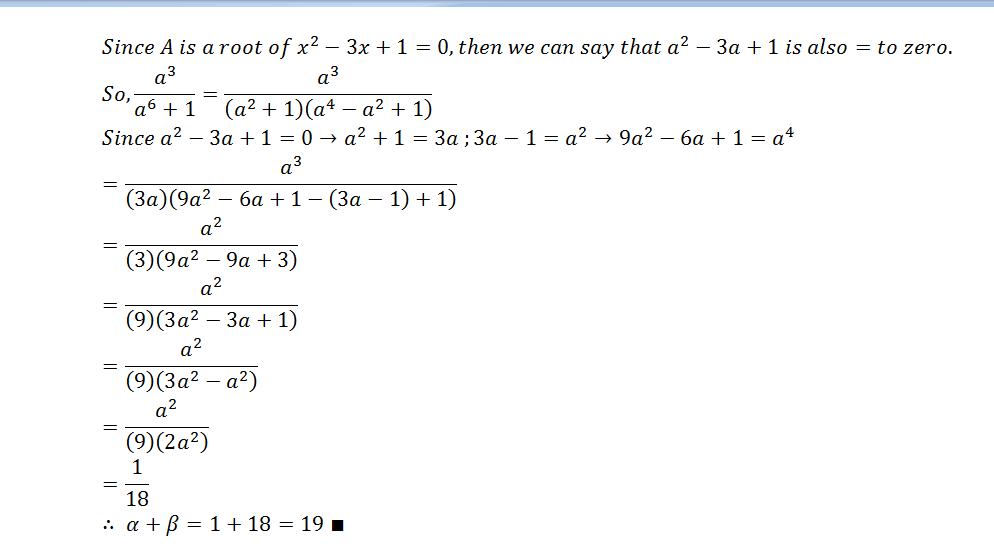
Let a,b be the 2 solns. Then a+b=3 and ab=1 ((a+b)^3)= a^3+b^3+3ab(a+b)... Substituting the values of a+b and ab, 18=a^3+b^3. 18=a^3+1/a^3 therefore a^3/1+a^6=1/18 therefore 1+18=19
So a 2 + 1 = 3 a
and this gives:
a 2 + 1 a = 3 1 ,
and
( a 2 + 1 ) 2 = 9 a 2 ⟹ a 4 + 1 = 7 a 2 .
So
a 4 − a 2 + 1 a 2 = 6 a 2 a 2 = 6 1 . And finally
a 6 + 1 a 3 = a 2 + 1 a ⋅ a 4 − a 2 + 1 a 2 = 3 1 ⋅ 6 1 = 1 8 1 .
@Mehul Chaturvedi Why don't you make a set of these good problems - Are you smater than me thanks
- Using the quadratic formula the roots are 2 3 ± √ 5
- pick one of the roots a = 2 3 + √ 5 to substitute into a ⁶ + 1 a ³
- a³ = 9+4√5
- a⁶+1 = 162+72√5 = 18(9+4√5)
- therefore β α = 1 8 1
- and α+β=19
A word of caution by me: Got it right in my second try! as Vikram Waradpande did, i too computed (a^3)+(1/a)^3 and got final [ a^3/a^6+1] as 1/18! But Your eyes must be good! root is a and we need to find (alpha)+(beta) don't treat alpha and a the same!
a 3 a 6 + 1 = a 3 + a 3 1 = ( a + a 1 ) 3 − 3 ( a + a 1 ) .
Now, since a is a root of the given equation, we get = a 2 + 1 = 3 a or a + a 1 = 3 Plugging this value, we get a 3 a 6 + 1 = 1 8 . Now all we want is it's reciprocal.