Are you smarter than me? 51
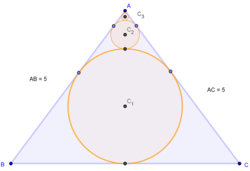 Let
be an isosceles triangle with
and
.Consider the sequence of circles
Having centres at
.Just like given given above . Then the area of part excluding circle's area+Radius of second circle is:
Let
be an isosceles triangle with
and
.Consider the sequence of circles
Having centres at
.Just like given given above . Then the area of part excluding circle's area+Radius of second circle is:
The answer is 4.835.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Inradius r is given by: r = s ( s − a ) ( s − b ) ( s − c ) , where a , b and c are the side lengths of the triangle and s = 2 a + b + c .
Therefore, the radius of circle centered C 1 :
r 1 = 8 ( 8 − 6 ) ( 8 − 5 ) ( 8 − 5 ) = 8 2 × 3 × 3 = 2 3
We note that C 1 , C 2 and C 3 are aligned on a same straight line. They are incircles of similar triangles.
And we note that: r 1 r 2 = 4 4 − 2 r 1 = 4 1 .
Similarly, r 2 r 3 = 4 1 ⇒ r 2 = 8 3 ⇒ r 3 = 3 2 3
The required result:
2 1 × 6 × 4 − π ( r 1 2 + r 2 2 + r 3 2 ) + r 2
= 1 2 − π ( ( 2 3 ) 2 + ( 8 3 ) 2 + ( 3 2 3 ) 2 ) + 8 3 = 4 . 8 3 7