Are you smarter than me?

Here is a way to tackle the problem using vectors-

---

---

We are given that $\left|\vec{b}\right|=\left|\vec{c}\right|$ . Also, $|\vec{BC}|=|\vec{BD}|=2$ .

$\begin{aligned} |\vec{BD}|=2 \implies \left|\dfrac{\vec{c}}{2}-\vec{b}\right|&=2\\ \left|\dfrac{\vec{c}}{2}-\vec{b}\right|^2&=4\\ \left(\dfrac{\vec{c}}{2}-\vec{b}\right) \cdot \left(\dfrac{\vec{c}}{2}-\vec{b}\right)&=4 \ \ \ \ \ \ \ \ \ \ \because |\vec{r}|^2=\vec{r} \cdot \vec{r}\\ \dfrac{\left|\vec{c}\right|^2}{4}-\dfrac{\left|\vec{b}\right| |\vec{c}| \cos{A}}{2}-\dfrac{\left|\vec{b}\right| |\vec{c}| \cos{A}}{2}+\left|\vec{b}\right|^2&=4\\ \dfrac{5|\vec{c}|^2}{4}-|\vec{c}|^2 \cos{A}&=4 \ \ \ \ \ \ \ \ \ \ \because \ |\vec{c}|=\left|\vec{b}\right|\\ \cos{A}&=\dfrac{5}{4}-\dfrac{4}{|\vec{c}|^2}\\ \end{aligned}$

---

But, $\cos{A}=\dfrac{2|\vec{c}|^2-4}{2|\vec{c}|^2}$ due to the law of cosines .

So, $1-\dfrac{2}{|\vec{c}|^2}=\dfrac{5}{4}-\dfrac{4}{|\vec{c}|^2} \implies |\vec{c}|^2=8 \implies \cos{A}=\dfrac{3}{4} \implies \sin{A}=\dfrac{\sqrt{7}}{4}$

---

Lastly, $\text{Area of} \ \triangle ABC=\dfrac{1}{2}\left|\vec{b} \times \vec{c}\right|=\dfrac{1}{2} \cdot 8 \cdot \dfrac{\sqrt{7}}{4}=\boxed{\sqrt{7}}$

$Two ~ isosceles ~\Delta s ~ABC~\cong~BDC~ since~they~have~the~same~ common~equal~\angle C.\\ \therefore~\dfrac{AB}2=\dfrac{BC}{DC},~~\implies~\dfrac{AB}2=\dfrac 2{\frac{AB}2}.\\ \implies~AB=2\sqrt2. \\ \therefore~using~Hero's~on~\Delta~ABC, ~~S=\dfrac{2\sqrt2+2\sqrt2 + 2} 2=2\sqrt2+1.\\ Area~\Delta~ABC=\sqrt{(2\sqrt2+1)*1*1*(2\sqrt2-1)}=\sqrt{8 - 1}=~~~~\Large \color{#D61F06}{2.6458}$ $\large OR$

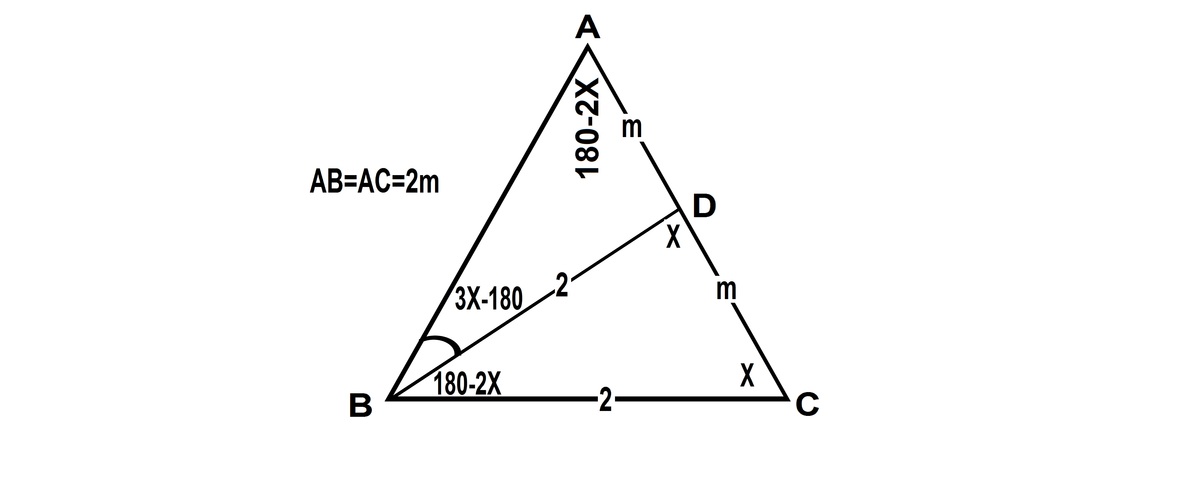
$If ~ \angle C=X, \text{all angles of the isosceles }\Delta s~are~given~in~ sketch.~~~Let~AB=AC=2m.\\ Applying ~ Sin ~ Law ~to~\Delta s ~ ADB ~ and ~ CDB,\\ \dfrac{Sin(3X-180)}{Sin(180-2X)}=\dfrac {AD}{BD} =\dfrac m 2 =\dfrac {AD}{CD}=\dfrac {Sin(180-2X)}{Sin(X)}\\ \implies ~ \dfrac { - Sin(3X)}{Sin(2X)}=\dfrac {Sin(2X)}{Sin(X)}\\$ $....................Note:-~~Sin(2X)=2*Sin(X)*Cos(X),~~Sin(3X)=3*Sin(X) - 4*Sin(X)^3.\\ Substituting ~ and ~ solving ~ taking ~ care ~ of ~ negative ~ sign ~we ~ get~~X= 69.295^o.\\$ $\text{Since D is the midpoint of AC, } area~ \Delta~ABC=area~2*\Delta~BDC=2*2*Sin(X)*2*Cos(X)\\ =~~~~\Large \color{#D61F06}{2.6458}$

$Let\quad AB=AC=x\quad \quad \quad \therefore \quad DC=AD=\frac { x }{ 2 } \\ Now\quad acc.\quad to\quad Apollonius\quad th.:\\ { \Longrightarrow \quad BC }^{ 2 }+AB^{ 2 }=2(BD^{ 2 }+{ DC }^{ 2 })\\ \Longrightarrow \quad 4+{ x }^{ 2 }=2(4+\frac { x^{ 2 } }{ 2 } )\\ \Longrightarrow \quad x\quad =\quad 2\sqrt { 2 } \\ \Longrightarrow \quad ar(\Delta )=\frac { a\sqrt { 4b^{ 2 }-a^{ 2 } } }{ 4 } \quad \quad \quad \quad [where\quad a=2,b=x]\\ \Longrightarrow \quad ar(\Delta )=\sqrt { 7 } \\ \\$

apolanius,, BC^2+AB^2=2 (BD^2+DC^2) 4+(2DC)^2=2 (4+DC^2) 4+4DC^2=8+2DC^2 2DC^2=4 so, DC=2√2 and the rest is easy

ac=sec A triangles abc similar to cbd sec A/2=2/(sec A/2) sec^2A=8 secA= 2 2^1/2=ac therefore altitude is root 7 by hypotenuse thm. area is 1/2 2*root7 answer is root 7 =2.645