Are you sure of your value?

Geometry Level pending

There is a constant C, independent of $n$ , such that if $\{z_j\}$ are complex numbers and if

$\sum_{j=1}^n |z_j| \geq 1,$

then there is a sub-collection $\{z_{j=1},...,z_{j_h}\}\subseteq\{z_1,...,z_n\}$ such that

$\Bigg | \sum_{m=1}^{k} z_{j_m} \Bigg | \geq C.$

What is the best (largest) constant $C$ ?

For example, we can surely allow $C=0$ and have the necessary equations always satisfied, but would that be the largest value?

taken from 'Function Theory of One Complex Variable' by Robert Greene

The answer is 0.3183.

1 solution

Milly Choochoo
Sep 17, 2014

The best constant $C$ is $\frac{1}{\pi}$ .

Proof:

We would like to find the largest number $C$ such that for any set of countable complex numbers whose sum of its constituent element's magnitudes is equal to $1$ , there will always be a subset of that set whose magnitude of the sum of its constituent elements is no less than $C$ .

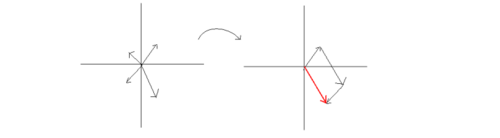
Interpreted geometrically, we have a bunch of arrows that, when you add up all of their lengths (magnitudes), gives you at least $1$ . You can take a sub-bunch of that bunch of arrows, position them all head to tail with one another, and then draw a line from the beginning of the first arrow and the tip of the last one and calculate the distance (magnitude) of that line.

[Look at the picture in the problem statement.]

To begin, we try to find the exact configuration of arrows (set of complex numbers) that minimizes the largest distance we can achieve by lining up a subset of that set. This naturally places the restriction $\sum_{j=1}^n |z_j| = 1$

on the optimal (worst actually) set we are trying to make.

Next, we would like to think of the set that minimizes the amount of 'arrow' in any particular direction, because too many arrows in the same direction would allow for a larger subset. In fact, what we are trying to do here is minimize the arc-length (sum of the magnitudes) and largest distance (magnitude of the sums) ratio. This will require maximizing the deviance/preference of the angle between any and all arrows, as well as minimizing the length of any arrow in any particular direction.

To satisfy these two requirements, clearly a regular polygon will maximize the deviance of the angles between the arrows, and making an arbitrarily large number of arrows of equal length would minimize the length of any arrow (or magnitude of the sum of any arrows) in any particular direction. These two requirements force our optimal/worst set of arrows to converge to that of which when lined up head to tail form a circle whose circumference is $1$ , and hence the largest line that can be made by configuring any portions of that circle (without changing their relative angle of course) would be $\frac{1}{\pi}$ , its diameter. $\blacksquare$

Woah, thats a lot of explaining. Reminds me of mr.chap's explanation on elementary particle physics. It was something about blowing something

Oscar Garcia - 6 years, 2 months ago

Are you sure of your value?

The answer is 0.3183.

1 solution

0 pending reports