Area
 In the rectangle shown above, if the area of the green region is 25, what is the area of the blue region?
In the rectangle shown above, if the area of the green region is 25, what is the area of the blue region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Split the green triangle into 2 right triangles.You will see that the triangles will be equivalent in size to the other corresponding blues so the blues and the greens must be equal.
The area of the green triangle = (1/2)bh = 25. Let the top side of the rectangle be split into x and b - x, each being met by the green triangle vertex Then the blue area = (1/2)bx + (1/2)x(b - x) = (1/2)bh = 25. Ed Gray
Let the base the triangle be b and its height be h . Then, we have:
A r e a o f t h e t r i a n g l e = 2 1 × b × h = 2 5
⇒ b × h = 5 0 . So, the area of the rectangle is 50.
∴ A r e a o f t h e b l u e r e g i o n = A r e a o f t h e r e c t a n g l e − A r e a o f t h e g r e e n r e g i o n = 5 0 − 2 5 = 2 5 .
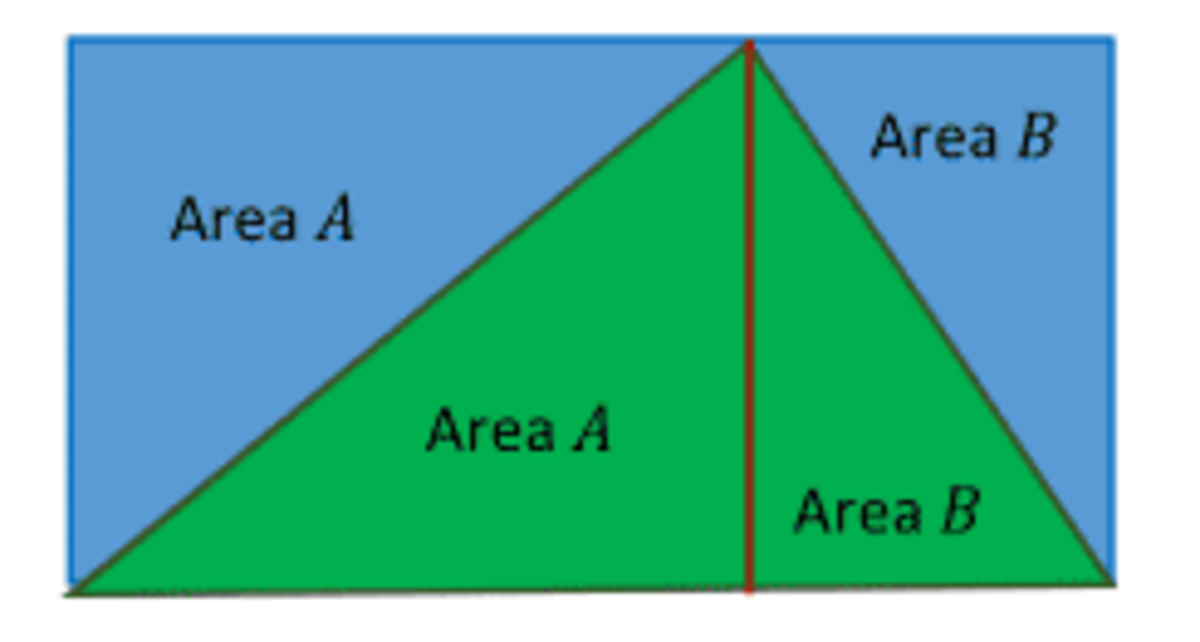
W e k n o w , i f a △ a n d a P a r a l l e l o g r a m l i e o n t h e s a m e b a s e a n d b e t w e e n s a m e p a r a l l e l s
t h e n A r e a o f △ = 2 1 × A r e a o f P a r a l l e l o g r a m
⇒ A r e a o f g r e e n r e g i o n = 2 1 × A r e a o f R e c t a n g l e
⇒ A r e a o f b l u e r e g i o n + A r e a o f g r e e n r e g i o n = A r e a o f R e c t a n g l e
∴ A r e a o f b l u e r e g i o n = A r e a o f g r e e n r e g i o n = 2 5