Area

Find $cosB$ using cosine rule which is $cosB=\dfrac{3}{4}$

Connect G and D then EFGD is a trapezium as $GF || ED$ .

As triangle ABG is right-angled so, using the value of cosB we can find BG=54 and AG= $18 \sqrt{7}$ .

As D and E are mid-points of AB and AC then $DE || BC$ and BF=DE=60/2=30

So, $BG=DE+FG=54$

The height is also divided at midpoint because $DE || BC$ and D is the mid-point of AC.

So, height of trapezium is $AG/2=9 \sqrt{7}$

So, area of trapezium is $\dfrac{1}{2} (DE+FG) \times 9 \sqrt{7}=\dfrac{1}{2} \times 54 \times 9 \sqrt{7}=243 \sqrt{7}$

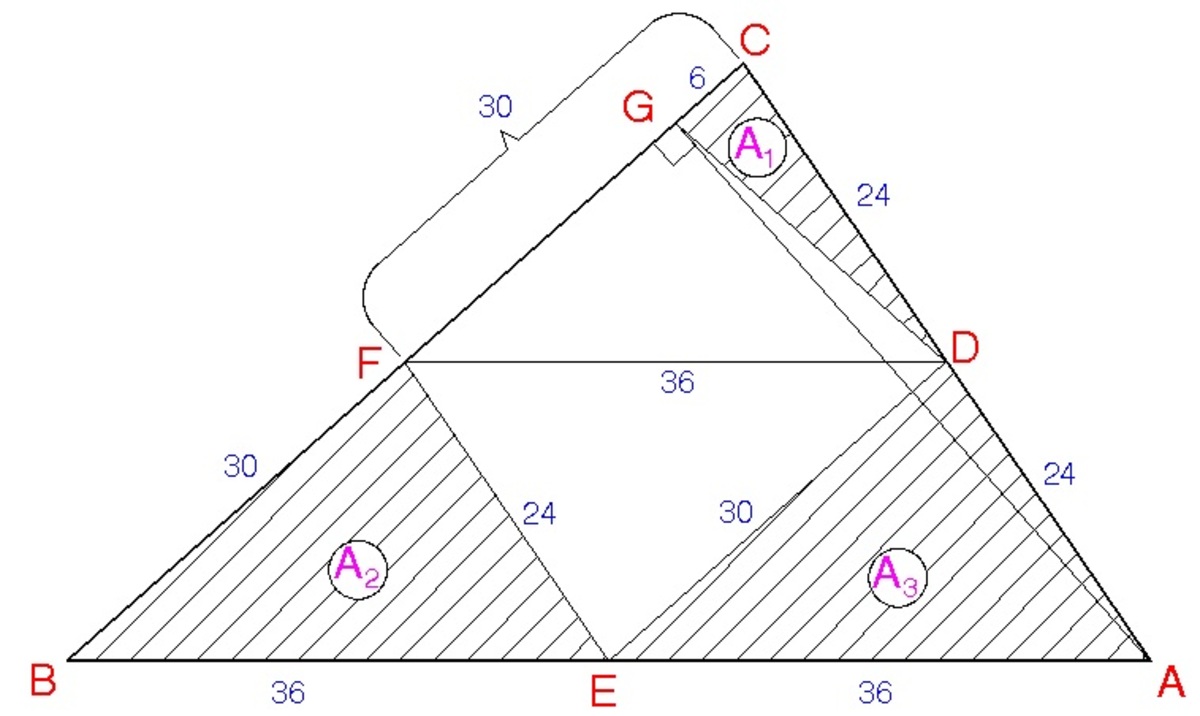Draw $GD$ to form trapezoid $EFGD$ .

$GD$ is the median to hypotenuse $CA$ of right $\triangle AGC$ . Therefore, $GD=\dfrac{1}{2}AC=\dfrac{1}{2}(48)=24$ .

$EF=\dfrac{1}{2}AC=\dfrac{1}{2}(48)=24$ $\large ;$ $ED=\dfrac{1}{2}BC=\dfrac{1}{2}(60)=30$ $\large ;$ $FD=\dfrac{1}{2}AB=\dfrac{1}{2}(72)=36$

Apply pythagorean theorem on $\triangle AGC$ and $\triangle AGB$ . $AG^2=48^2-CG^2$ and $AG^2=72^2-(60-CG)^2$ . We find $GC=6$

Compute $A_1$ $\large :$ $\color{#D61F06}\implies$ $s=\dfrac{24+24+6}{2}=27$ $\color{#3D99F6}\implies$ $A_1=\sqrt{27(27-24)(27-24)(27-6)}=\sqrt{5103}=27\sqrt{7}$

Compute $A_2$ $\large :$ $\color{#D61F06}\implies$ $s=\dfrac{30+24+36}{2}=45$ $\color{#3D99F6}\implies$ $A_2=\sqrt{45(45-30)(45-24)(45-36)}=\sqrt{127575}=135\sqrt{7}$

Compute $A_3$ $\large :$ $\color{#D61F06}\implies$ $A_3=A_2=135\sqrt{7}$

Compute area of $\triangle ABC$ $\large :$ $\color{#D61F06}\implies$ $s=\dfrac{60+48+72}{2}=90$ $\color{#3D99F6}\implies$ $A_{ABC}=\sqrt{90(90-60)(90-48)(90-72)}=\sqrt{2041200}=540\sqrt{7}$

Finally,

$A_{EFGD}=A_{ABC}-A_1-A_2-A_3=540\sqrt{7}-27\sqrt{7}-135\sqrt{7}-135\sqrt{7}=243\sqrt{7}$

It follows that,

$a+b=243+7=250$

$AB=60=12*5,~BC=72=12*6,~AC=48=12*4.~~~~~~Area~of~ABC~\frac 1 4*12^2* \sqrt{15*5*7*3}=540\sqrt7.\\ \therefore~AG=2*\dfrac{540\sqrt7}{60}=18\sqrt7.\\ So~ in~AGC~by~Pythagorean ~Theorem,~CG=6.~~But~CF=\frac 1 2*60=30.\\ \therefore~Area~CGD=\frac 6 {30}*Area~CFD=\frac1 5*Area~CFD.\\ Easy~to ~see~Area~CFD=Area~DFE=\frac 1 4*Area~ABC=135\sqrt7.\\ Area~EFGD=Areas~CFD+DFE-CGD=\Big(135+135-\dfrac{135} 5\Big)*\sqrt7=243\sqrt7=a\sqrt b.\\ So~Area~EFGD=\Large~~\color{#D61F06}{250}.$