Area
The figure below is a regular octagon.
Which area is larger, green or yellow?
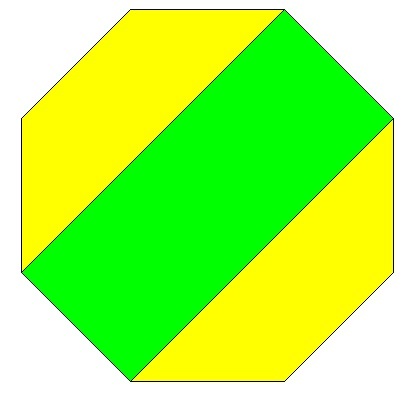
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
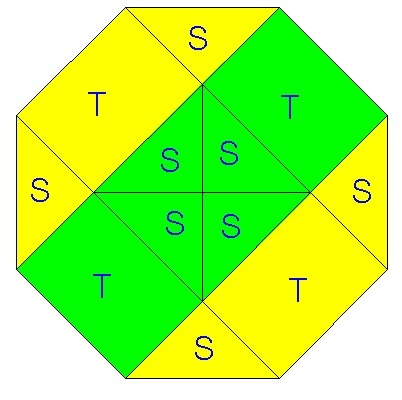The green region and the yellow region have been partitioned into smaller congruent regions and we can see that the areas of the green region and yellow region are the same size.
@Marvin Kalngan How do we identify whether the figure can be partitioned into smaller figures and if it can be then how do we proceed in partitioning?
Log in to reply
The best way is to draw the octagon true to scale. Then partition it as what Marvin did above. In partitioning, I think we need to do some experiments (many trials) because we need to measure the lines if they are equal. The most accurate way of solving this problem is to set a value for the length of one side of the regular octagon. Then calculate the areas by any method.
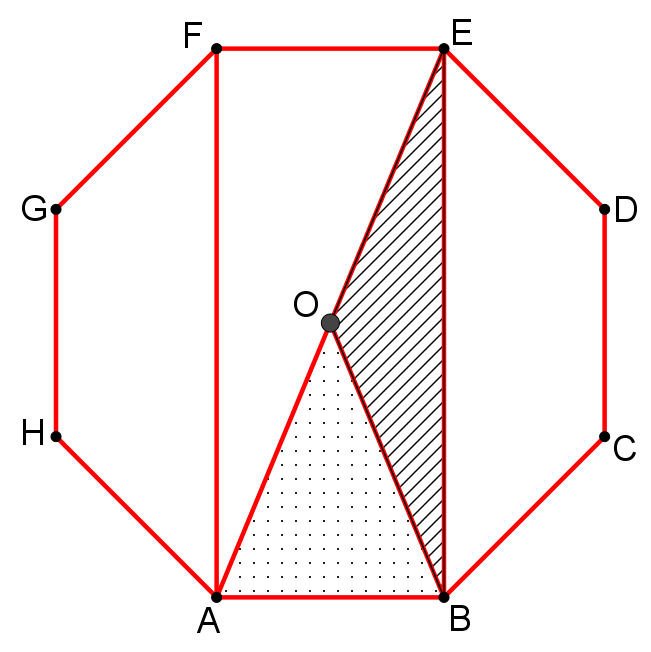
Let O be the middle of the octagon. Then [ A B O ] = 8 [ A B C D E F G H ] (because symmetry). Each angle of the octagon is 8 6 ∗ 1 8 0 ° = 1 3 5 ° degrees, so by calculating we get that the A B E F quadrilateral is a rectangle, and that mean [ A B E ] = [ A E F ] . Since A O = E O , the B O is a median of the A B E triangle, so [ A B O ] = [ B O E ] . Therefore
[ A B E F ] = 4 ∗ [ A B O ] = 2 [ A B C D E F G H ]
So the two area are equal.