Area after folding

Geometry Level 4

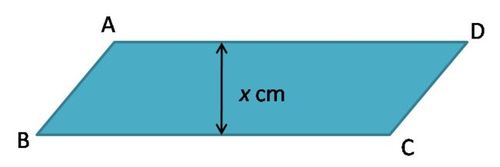In the figure, $ABCD$ is a parallelogram with the height of $x$ cm. It is known that $AB$ is 6 cm longer than the height and $AD$ is 3 cm longer than 4 times of the height.

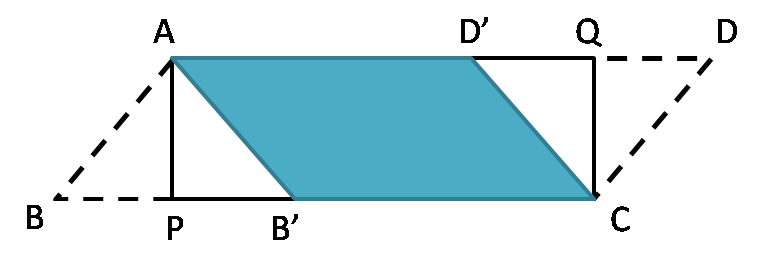
$AB$ and $CD$ are then folded along $AP$ and $QC$ respectively to form $AB'$ and $CD'$ respectively. Similarly, $BP$ and $QD$ are folded along $AP$ and $QC$ respectively to form $PB'$ and $QD'$ .

It is known that $AB'CD'$ is a rhombus, find the area of $AB'CD'$ .

Note: The figures are not drawn to scale.

The answer is 135.

2 solutions

Ratul Pan
Sep 28, 2015

given, AP=x , AB=x+6 , AD=4x+3
By pythagoras theorem,
$AB^2$ = $PB^2$ + $AP^2$
or, $(x+6)^2$ = $x^2$ + $PB^2$
Therefore, $PB^2$ = $\sqrt{36+12x}$
By congruency, BP = PB'
B'C = BC - (2BP) = AB' = AB = Side of rhombus
x+6 = 4x+3 - 2 $\sqrt{36+12x}$
or, 2 $\sqrt{36+12x}$ = 3x - 3 squaring both side,
or, 144 + 48x = 9 $x^2$ + 9 -18x
or, -9 $x^2$ + 66x + 135 = 0
or, -3 $x^2$ + 22x +45 =0
or, (9-x)(5+3x) = 0
or, x = 9
Therefore B'C=15
Area = 15 * 9
=135

Niranjan Khanderia
Oct 3, 2015

$AP=X,~~AB=AB'=\color{#3D99F6}{B'C = X+6},~~BC=4X+3.\\ \therefore~ BB' = BC - B'C= 3X - 3.~~~\implies~PB' = \dfrac{3X - 3}2.\\ AB'^2 = AP^2 + PB'^2,~~\implies~(X + 6)^2= X^2 + \left \{\dfrac{3X - 3} 2 \right \}^2.\\ \text{Solving the quadratic with +tive answer, X = 9.}\\ Area ~of~AB'CD' = (X + 6)*X = 15*9 = ~~~~~~~\Large \color{#D61F06}{135}$

Area after folding

The answer is 135.

2 solutions

0 pending reports