Area between a function and a rotation of its reflection.
Given is the function f ( x ) = sin ( x ) and a curve created as the reflection of f ( x ) in the x -axis after which it is rotated around O ( 0 , 0 ) by 45 degrees. A graph of the function and the curve can be seen below.
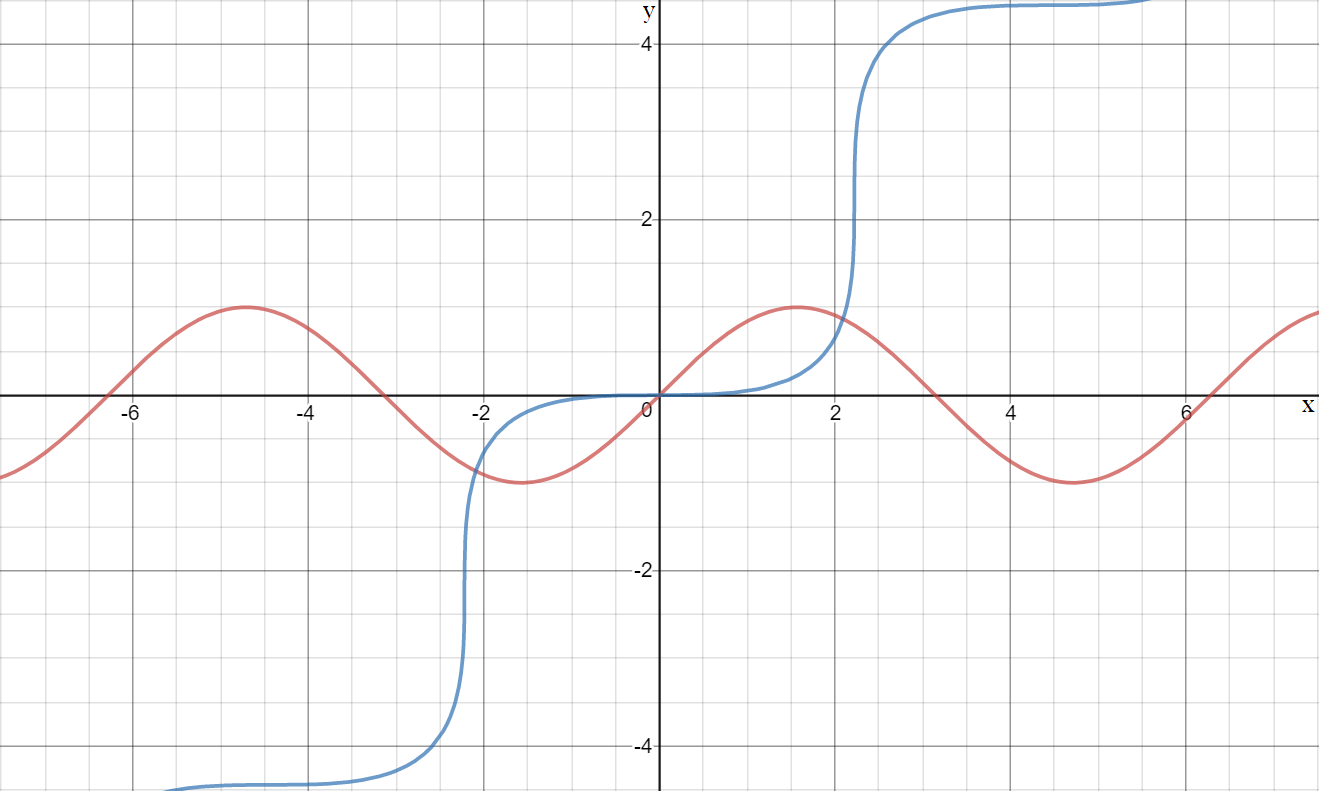
Let ξ be the x -coordinate of the intersection to the right and let A be the area bound by the function and the curve. Then, A = a ( b − cos ξ ) + c ( d − e ) ξ 2 , where a , b , c , d ∈ Z and e is prime. Calculate a ⋅ b ⋅ c ⋅ d ⋅ e .
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Dang it. got it wrong in the end due to my ignorance,for some reason i tried inputting the sum of a+b+c+d+e instead, awesome question though :)
also its much easier to solve for tan ( 8 π ) directly as,
tan ( 2 8 π ) ⟹ 2 x ⟹ ( x + 1 ) 2 x = 1 − x 2 2 x = 1 For x = tan ( 8 π ) = 1 − x 2 = 2 = 2 − 1 Disregard − ( 2 + 1 ) as tan ( 8 π ) > 0
Ah, that's unfortunate. However, thanks for sharing that information about tan(2x), I was not aware of that identity. I will change my solution accordingly, because I don't like that working out what tan(pi/8) equals takes longer than the rest of the calculation.
You could also use the half-angle formula tan 2 x = sin x 1 − cos x .
Log in to reply
Ah, that's another identity I wasn't aware of, and even simpler to calculate. Nice find!
Thanks for the interesting problem! I went the long way round, and worked out a parametric equation for the blue curve,
x = 2 t + sin t , y = 2 t − sin t
It was then possible to work out the area under this curve (the integral involves some integration by parts, but nothing non-standard; knowing that there is a more sensible symmetry argument makes that kinda obvious!) and subtract it from the area under the sine curve. But this wasn't as neat a solution as yours.
Log in to reply
Can you please elaborate how you did the integration?
isint the new function x-sinx
Log in to reply
How would you check? We can pick a point on the red curve, reflect and rotate it; let's choose ( π , 0 ) , as this is a pretty easy point to transform. Reflection in the x -axis doesn't change it; the rotation maps it to the point ( 2 π , 2 π ) , which is on the blue curve. It's easy to check that y = x − sin x for this point, so that cannot be the equation of the blue curve.
The parametric equation I wrote earlier was derived by applying the transformation in matrix terms as described in Joël Ganesh's solution to the curve ( t , sin t ) . I can't see any obvious simpler form, but that doesn't mean there isn't one.
Dude your problem is really hard I can't believe I could solve it. I'm 14 btw.
Let g be the new, reflected/rotated function. As stated by @Joël Ganesh , g is the reflection of f across the line y = ( tan 8 π ) x . To understand why this is so, think about what it means to reflect and rotate f : everything f does relative to the x -axis, g does relative to the 4 5 ∘ line, but in the opposite direction. Therefore, the two functions will literally meet halfway , on the line with half the angle from the x -axis compared to the 4 5 ∘ ( 4 π -radian) line--namely, the 2 2 . 5 ∘ ( 8 π -radian) line, whose slope is tan 8 π .
Using this information and the knowledge of the characteristics of sine curves, we can divide the area into four congruent regions as shown below:
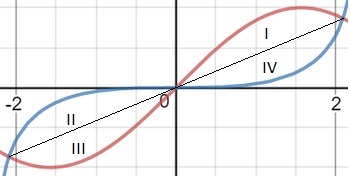
All four regions have the same area, which you can calculate by integrating the difference between f ( x ) and the line of reflection from 0 to ξ :
A = 4 ∫ 0 ξ sin x − ( tan 8 π ) x d x = 4 ( 1 − cos ξ ) − 2 tan 8 π ξ 2
Using the half-angle identity for the tangent function,
tan 8 π = 1 + cos 4 π 1 − cos 4 π = 1 + 2 2 1 − 2 2 = 2 + 2 2 − 2 ⋅ 2 − 2 2 − 2 = 4 − 2 ( 2 − 2 ) 2 = 2 2 − 2 ⋅ 2 2 = 2 2 ( 2 − 1 ) = 2 − 1 .
Therefore,
A = 4 ( 1 − cos ξ ) + 2 ( 1 − 2 ) ξ 2 ,
with a = 4 , b = 1 , c = 2 , d = 1 , and e = 2 .
It might be obvious or might be not, but the curve is a reflection of f ( x ) in the line y = tan ( π / 8 ) x . To derive at this mathematically, I will assume you know about the rotation matrix M r o t of a rotation around O by θ and the reflection matrix M r e f of a reflection around the line y = tan ( θ ) x : M r o t = ( cos θ sin θ − sin θ cos θ ) a n d M r e f = ( cos 2 θ sin 2 θ sin 2 θ − cos 2 θ ) . Consider a point P ( x p , y p ) ∈ R 2 which corresponds to a vector p ∈ R 2 . The transformation T : R 2 → R 2 given by a reflection in the line y = 0 after which it is rotated around O by 45 degrees will have the property that p ↦ ( cos ( π / 4 ) sin ( π / 4 ) − sin ( π / 4 ) cos ( π / 4 ) ) ( cos ( 0 ) sin ( 0 ) sin ( 0 ) − cos ( 0 ) ) p = ( cos ( π / 4 ) sin ( π / 4 ) sin ( π / 4 ) − cos ( π / 4 ) ) p . Note that the last matrix is exactly the matrix corresponding to a reflection in the line y = tan ( π / 8 ) x . So indeed, the curve is a reflection of f ( x ) in the line y = tan ( π / 8 ) x . Note that in general R o t ( θ ) ∘ R e f ( 0 ) = R e f ( θ / 2 ) , see Wikipedia .
Notice that the new information about the curve makes the problem much easier, because while we don't know what the formula is for the curve, we make the observation that A = 4 ⋅ ∫ 0 ξ ( sin ( x ) − tan ( π / 8 ) x ) d x , but before calculating this integral, note (thanks to Jon Haussman) that tan ( t / 2 ) = sin ( t ) 1 − cos ( t ) , and so we see that tan ( π / 8 ) = 2 − 1 . The method described by Anirudh Sreekumar in the comments will also work. Now back to integrating. We see that A = 4 ⋅ ∫ 0 ξ ( sin ( x ) + ( 1 − 2 ) x ) d x = − 4 cos ξ + 2 ( 1 − 2 ) ξ 2 + 4 = 4 ( 1 − cos ξ ) + 2 ( 1 − 2 ) ξ 2 . We can conclude that a ⋅ b ⋅ c ⋅ d ⋅ e = 4 ⋅ 1 ⋅ 2 ⋅ 1 ⋅ 2 = 1 6 .
For those who are curious, A ≈ 2 . 3 6 6 0 7 5 4 5 2 7 5 .