This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Is the drawing you drew? If it is true, you are bad at drawing. (But better than me.)
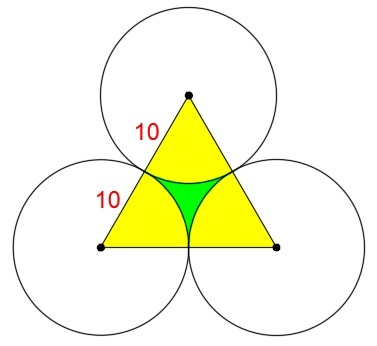 Consider my diagram. Connect the centers of the three circles to form an equilateral triangle of side length
2
0
. Observed that there are three sectors of a circle. If you add the areas of the three circular sectors, it would be the area of a semi-circle because the sum of the interior angles of a triangle is
1
8
0
∘
. So the area of the three circular sectors (yellow region is)
2
1
π
(
1
0
)
2
=
5
0
π
. The area of an equilateral triangle is given by
4
3
x
2
where
x
is the side length. So the area of the equilateral triangle is
4
3
(
2
0
)
2
=
1
0
0
3
. The area of the green part (shaded region in the problem) is equal to the area of the equilateral triangle minus the area of the yellow part. We have
Consider my diagram. Connect the centers of the three circles to form an equilateral triangle of side length
2
0
. Observed that there are three sectors of a circle. If you add the areas of the three circular sectors, it would be the area of a semi-circle because the sum of the interior angles of a triangle is
1
8
0
∘
. So the area of the three circular sectors (yellow region is)
2
1
π
(
1
0
)
2
=
5
0
π
. The area of an equilateral triangle is given by
4
3
x
2
where
x
is the side length. So the area of the equilateral triangle is
4
3
(
2
0
)
2
=
1
0
0
3
. The area of the green part (shaded region in the problem) is equal to the area of the equilateral triangle minus the area of the yellow part. We have
A = 1 0 0 3 − 5 0 π ≈ 1 6 . 1 2 5 4 4 8 0 8
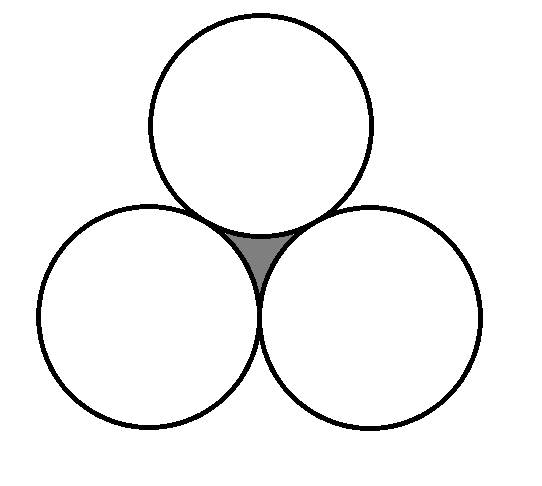
Let the centers of the three circles be joined so as to form an equilateral triangle of side, a .
Area of this triangle is given to be A = 4 3 a 2
The formation of such a triangle forms sectors in each circle. These sectors are alike since radii of the circles is the same i.e ( 2 a )
The area of such sectors is given by A = 2 1 ( 0 . 5 a ) 2 θ
Area of the required region is simply given by
4 3 a 2 − 3 2 1 ( 0 . 5 a ) 2 θ
Now since it is an equilateral triangle θ = 3 π and 0 . 5 a = 1 0 c m
Substituting these values we get the area of the region to be ≈ 1 6 c m 2